porównanie objętości.
Alan: Mamy dwa pojemniki: pierwszy ma kształt szescianu, drugi − ostrosłupa prawidłowego
czworokatnego. Przekatna szescianu ma długosc 6
√2 cm. Wysokosc ostrosłupa tworzy ze
sciana boczna kat o mierze 60° . Pole powierzchni bocznej ostrosłupa jest równe 64
√3 cm
2 .
Sprawdz na podstawie odpowiednich obliczen, czy woda wypełniajaca całkowicie pierwszy
pojemnik zmiesci sie w drugim pojemniku.
Mam problem z obliczeniem niewiadomych Pb − krawędzi bocznej i wysokości ściany bocznej.. Jak
wyznaczyć 2 niewiadome mając jedynie Pb.. gdyby to jeszcze był czworościan foremny to wysokość
jak i krawędź wziąłbym z wzorów na pole trójkąta równobocznego a tu nie wiem jak to uzyskać..
Pozdrawiam

14 sty 12:49
krystek:
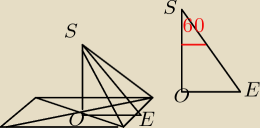
14 sty 13:08
Aga:
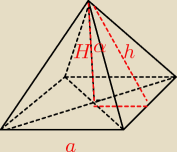
Musisz obliczyć V sześcianu i ostrosłupa.
P
b=2ah
P
b=64
√3
a*h=32
√3
sin60
0=U{
√3{2}
podstaw i rozwiąż układ równń
14 sty 13:12
ejendi:
sześcian:
(6√2)2=a2+(a√2)2
a=6
14 sty 13:15
14 sty 13:32
ejendi:
ostrosłup
Pb=a
2+2*hs*a, pole ostrosłupa anie trójkąta
hs=a/2sin60=a/
√3
64√3=a
2+2*a
2/
√3
h=a/(2
√3)
| | 1 | | 1 | | a3 | |
Vostr= |
| h*a2= |
| * |
| |
| | 3 | | 6 | | √3 | |
14 sty 13:42
Aga: @ejendi Twój wzór jest na pole powierzchni całkowitej ostrosłupa.
14 sty 13:50
ejendi:
zgadza się asz=6√2/√3=2√6
14 sty 13:55
ejendi: tak, w zadaniu jest Pole powierzchni bocznej ostrosłupa jest równe 64√3 cm2
14 sty 13:57

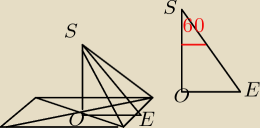
 Musisz obliczyć V sześcianu i ostrosłupa.
Pb=2ah
Pb=64√3
a*h=32√3
Musisz obliczyć V sześcianu i ostrosłupa.
Pb=2ah
Pb=64√3
a*h=32√3