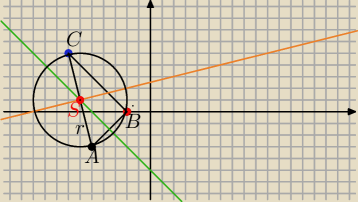
 A=(−5,−3)
B=(−2,0)
C=(−7,5)
Równanie symetralnej boku AB
(x+5)2+(y+3)2=(x+2)2+(y−0)2
x2+10x+25+y2+6y+9=x2+4x+4+y2
6x+6y+30=0
6y=−6x−30
y=−x−5
−−−−−−−−−−−−−−−
Równanie symetralnej boku AC
(x+5)2+(y+3)2=(x+7)2+(y−5)2
x2+10x+25+y2+6y+9=x2+14x+49+y2−10y+25
−4x+16y−40=0
16y=4x+40
A=(−5,−3)
B=(−2,0)
C=(−7,5)
Równanie symetralnej boku AB
(x+5)2+(y+3)2=(x+2)2+(y−0)2
x2+10x+25+y2+6y+9=x2+4x+4+y2
6x+6y+30=0
6y=−6x−30
y=−x−5
−−−−−−−−−−−−−−−
Równanie symetralnej boku AC
(x+5)2+(y+3)2=(x+7)2+(y−5)2
x2+10x+25+y2+6y+9=x2+14x+49+y2−10y+25
−4x+16y−40=0
16y=4x+40
| 4 | 40 | |||
y= | x+ | |||
| 16 | 16 |
| 1 | 5 | |||
y= | x+ | |||
| 4 | 2 |
| 1 | 5 | |||
−x−5= | x+ | |||
| 4 | 2 |
| 1 | 1 | |||
−1 | x=7 | |||
| 4 | 2 |
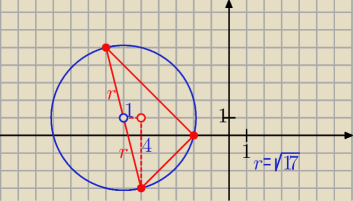 A(−5, −3), B(−2, 0), C(−7, 5), x2 + y2 + ax + by + c = 0
B: 4 + 0 − 2a + 0 + c = 0 ⇒ c = 2a − 4
A: 25 + 9 − 5a − 3b + c = 0 ⇒ 34 − 5a − 3b + 2a − 4 = 0 ⇒ 3a + 3b = 30 ⇒ b = 10−a
C: 49 + 25 − 7a + 5b + c = 0 ⇒ 74 − 7a + 5b + 2a − 4 = 0 ⇒ −5a+5b =−70 ⇒ b = a−14
a − 14 = 10 − a ⇒ 2a = 24 ⇒ a = 12, b = 10 − 12 = −2, c = 2*12 − 4 = 20
równanie okręgu: x2 + y2 + 12x − 2y + 20 = 0 ⇒ (x + 6)2 + (y − 1)2 = 17
A(−5, −3), B(−2, 0), C(−7, 5), x2 + y2 + ax + by + c = 0
B: 4 + 0 − 2a + 0 + c = 0 ⇒ c = 2a − 4
A: 25 + 9 − 5a − 3b + c = 0 ⇒ 34 − 5a − 3b + 2a − 4 = 0 ⇒ 3a + 3b = 30 ⇒ b = 10−a
C: 49 + 25 − 7a + 5b + c = 0 ⇒ 74 − 7a + 5b + 2a − 4 = 0 ⇒ −5a+5b =−70 ⇒ b = a−14
a − 14 = 10 − a ⇒ 2a = 24 ⇒ a = 12, b = 10 − 12 = −2, c = 2*12 − 4 = 20
równanie okręgu: x2 + y2 + 12x − 2y + 20 = 0 ⇒ (x + 6)2 + (y − 1)2 = 17


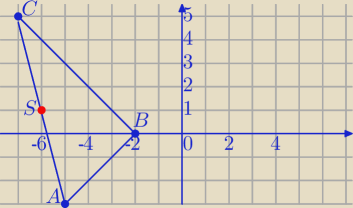 A=(−5,−3) ,B=(−2,0) C=(−7,5)
AB→=[3,3], B→=[−5,5],AC→=[−2,8]
[3,3] o[−5,5]=3*(−5)+3*5=0
ΔABC−Δprostokątny
A=(−5,−3) ,B=(−2,0) C=(−7,5)
AB→=[3,3], B→=[−5,5],AC→=[−2,8]
[3,3] o[−5,5]=3*(−5)+3*5=0
ΔABC−Δprostokątny
| −5+(−7) | −3+5 | |||
S=( | ; | )=(−6, 1)− środek przeciwprostokątnej | ||
| 2 | 2 |