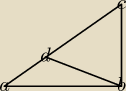
oblicz pole trojkata michal: witam,nie wiem czy corka dobrze zapamietala ale przekazala mi,ze na klasowce mialo zadanie: ab=4 bc=3 ad=1.5 dc=3.5 abc jest trojkatem prostokatnym oblicz pole trojkata bdc dziekuje i pozdr

Rivek: w takim razie ac=ad+dc=3.5+1.5=5 jest to najdłuższy bok, więc jest przeciwprostokątną, więc pole to P=¹₂*ab*bc=¹₂*4*3=6

Rivek: a, trójkąt bdc to chwilka

Rivek: Wzór na pole trójkąta to jest U{1]{2}dc*bc*sinα α−kąt pomiędzy tymi bokami dc bc. A z tego

	ab
trójkąta całego abc mamy sinα=		=4/5
	ac

więc

	4
P=12*3.5*3*		=..
	5

nie wiem jaki sposób córka umiała

michal: corka jest w 6 klasie wiec chyba cos namieszala,mi sie juz glowa zapalila

michal: dzisiaj odebrala klasowke i wszystko sie zgadza,czy ktos da rade rozwiazac zadanie z 6 klasy podstawowki?

michal: mozemy uzyc tylko podstawowych wzorow na pole trojkata rownolegloboku czy trapezu,pitagorasa jeszcze nie miala

nik: oblicz a1 i r w ciagu aretmetycznym takim ze a1 = 16 , a5=8

Basia: metodami z podstawówki chyba nie, ale jeszcze pomyślę

AC: S_ABD+ S_BDC= 6

SABD		1
	=
SBDC		2

⇔ S_BDC= 4

AC: Poprawka

SABD		1,5
	=
SBDC		3,5

S_BDC = 0,7 * 6 = 4,2

michal: co to jest S?

AC: Pole trójkąta

pomagacz:

	ab * bc		ac * h
P =		=		gdzie h to wysokość poprowadzona na bok ac
	2		2

policzysz h to podstawisz do wzoru:

	dc * h
P =
	2

pomagacz: Trudne? Nie, tylko trzeba użyć wyobraźni

michal: czyli ciagow i sin nie musiala jednak znac,dziekuje pomagacz

pomagacz: nie ma za co

michal: ciekawi mnie jeszcze jak to wyliczyl/la AC bo nie lapie

pomagacz: ac = ad + dc

michal: chodzilo mi o uzytkownika AC i jego obliczenia

AC: Trójkąty ΔABD i ΔBDC mają wspólną wysokość, stąd stosunek pól jest równy stosunkowi podstaw, czyli S{ABD} : S{BDC} = AD: DC

michal: dziekuje za pomoc,pozdrawiam

Basia: AC gdzie jest ta wspólna wysokość ? P_bcd = ¹₂*⁷₂*3*³₅ (tak jak policzył Rivek) = ^7*9₂₀ = ⁶³₂₀ = 3,15

Basia: sorry P = ¹₂*{7}{2}*3*{4}{5} = ²¹₅ = 4,2 ale nadal nie widzę naprawdę tej wspólnej wysokości

Basia: a ta na bok ac ma być, faktycznie już widzę

Mila: Klasa VI.

	3∧4
PΔABC =		=6
	2

	5∧h
PΔABC =		=6
	2

	5
h = 6:
	2

	12
h=
	5

Tę samą wysokość ma ΔBDC

	1		12
PΔBDC =		∧3,5 ∧
	2		5

BLAZEJ_505: można też ze wzoru Herona

krystek: @Błażej klasa VI ,nie ten etap!