wyznacz kąt miedzy tworząca stożka, nr 2 oblicz odleglosc srodka kola
Elfik: pole podstawy stozka jest rowne 27 π cm2 a jego V=27 cm3 wyznacz kąt miedzy tworzącą
stożka a jego podstawą.
zadanie nr 2.
Kule o promieniu 5 cm przecieto plaszczyzna, otrzymany przekroj jest kolem o polu rownym
16π cm2. Oblicz odleglosc srodka tego kola od srodka kuli.
prosze o pomoc
26 mar 19:33
seb: πr2=27π πr2=16π
r2=27 r=4
r=√27=3√3 s=√52−42
27π=27π*H/3 s=3
H=3
tgα=√3/3
α=30o
29 mar 20:05
natatalaka: Przekatna przekroju osiowego walca ma długość d i tworzy z płaszczyzna podstawy kat
α.Oblicz objetosc walca.
30 mar 11:58
natatalaka: Dany jest walec i kula o promieniu równym promieniowi podstawy walca.Objetośc obu brył sa
jednakowe.Pole powierzchni całkowitej walca jest równe 42π.Wyznacz długość promienia
podstawy i wysokosc walca.
30 mar 12:01
natatalaka: Z urny w której sa 3kule białe i 5czarnych,wylosowano 3kule.Oblicz prawdopodobienstwo ,ze
wylosowano kule jednokolorowe.
30 mar 12:03
natatalaka: Rzucamy dwa razy symetryczną sześcienna kostka do gry.Oblicz prawdobodobienstwo kazdego
z nastepujacych zdarzen
a) A−w kazdym rzucie wypadnie nieparzysta liczba oczek,
b)B−suma oczek otrzymanych w obu rzutach jest liczba wieksza od 9,
c)C−suma oczek otrzymanych w obu rzutach jest liczba nieparzysta i wieksza od 9.
witam,dałoby rade sie moje zadania dzis rozwiazac?potrzebuje na jutro a dzis dopiero
przypadkowo trafiłam na te stronke
30 mar 12:11
tim: Ok. Pomagam w II.
V
walca = πr
2h
P
cwalca = 2πr(r+h)
| | 4 | |
{ |
| πr3 = πr2h Vkuli = Vwalca |
| | 3 | |
{ 2πr(r+h) = 42π P
cwalca = 42
Mamy układ równań. Rozwiązujemy.
{ 2πr(r+h) = 42π /:2π
{ r(r+h) = 21
Podstawiamy h do drugiego.
r
2 = 9
r = 3
Podstawiamy r do wzoru i obliczamy h.
{ 3(3+h) = 21
9 + 3h = 21
12 = 3h
h = 4
Odp: r = 3 h = 4
30 mar 12:11
tim: Jedno masz

30 mar 12:11
tim: Reszta, to już nie moja "dziedzina" więc pewnie później "ktoś" pomoże.
30 mar 12:12
Kasia: Jaką objętość ma kula, której pole powierzchni całkowitej ma 64π?
Pc=64π
4πr
2=64π /:4
r
2=16
r=4
V=85,33πcm3
Odp.Objętość kuli wynosi 85,33πcm3
Proszę o poprawienie błędów.
3 lis 17:20
3 lis 17:36
Kasia:

Przekrój osiowy walca jest kwadratem o boku długości 4. Wyznacz objętość walca.
V=π(4)
2 * 4
√3
V=π*16*4
√3
V=64
√3πcm3
l=16
h=4
√3
r=4
odp. Objętość stożka wynosi 64
√3πcm3
3 lis 17:59
Kasia:
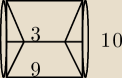
Podstawy trapezu równoramiennego mają dł. 9 i 3 a kąt ostry trapezu ma 60stopni. Oblicz
objętość bryły powstałej w wyniku obrotu tego trapezu do okoła krótszej postawy.
h=9
r=5
V=?
3
2 +9
2 = c
2
9+81=c
2
c
2=100
c=10
V=πr
2*h
V=π5
2*9
V=π25*9
V=225π
Powstał walec i dwa stożki złączone podstawami.
3 lis 18:09
Kasia: Ktoś pomoże w zadaniach wyżej ? Sprawdzi i poprawi błędy?
3 lis 18:10
Wiola: 2. Przekrój osiowy stożka jest trójkątem równobocznym o boku dł 6√3. Oblicz pole
powierzchni bocznej tego stożka.
4. Pole powierzchni całkowitej stożka jest równa 48πcm2. Tworząca stożka jest 3 razy dłuższa
od
promienia podstawy. Oblicz długość promienia podstawy stożka i jego objętość.
5. Kąt rozwarcia stożka ma miare 120 stopni a jego wysokość równa 18 cm. Oblicz pole boczne
stożka.
Ktoś pomoże rozwiązać ?
3 lis 18:49
dero2005:
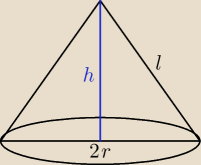
zad 2
l = 2r = 6
√3
P
b = πrl = π*3
√3*6
√3 = 54π
3 lis 19:35
dero2005:
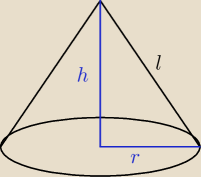
zad 4
P
c = πr(r+l) = 48π
l = 3r
πr(r + 3r) = 4πr
2 = 48π
r
2 = 12
r = 2
√3
l = 3r = 6
√3
h =
√l2 − r2 =
√108 − 12 =
√96 = 4
√6
3 lis 19:42
dero2005:
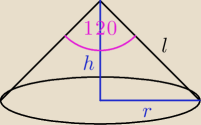
zad5
h = 18
r = h
√3 = 18
√3
l =
√h2 + r2 =
√182 + (18√3)2 =
√324 + 972 =
√1296 = 36
P
b = πrl = π*18
√3*36 = 648π
√3
3 lis 19:49
Wiolcia: 1. Przekrój osiowy stożka jest trójkątem równobnocznym, którego bok ma długość 4 cm. Oblicz
objętość i pole boczne stożka.
2. Przekrój osiowy walca jest kwadratem o przekątnej długości 2 √3 cm. Oblicz objętość i
pole całkowite walca.
3. Oblicz objętość kuli o polu powierzchni 16π.
4. Pole całkowite walca wynosi 785 cm2, pole boczne wynosi 628 cm2. Oblicz objętość walca.
5. Równoległobok o bokach długości 5 cm i 3 cm oraz kącie ostrym 60℃ obraca się wokół dłuższego
boku. Oblicz objętość i pole całkowite tej bryły.
Proszę o pomoc w rozwiązaniu tych zadań w jak najprostszy sposób.
1 gru 16:15
mała:
1. Wysokość walca jest dwa razy dłuższa od średnicy jego podstawy. Oblicz pole całkowite walca,
jeśli jego objętość wynosi 32π.
2. Po rozwinięciu powierzchni bocznej walca otrzymano kwadrat o przekątnej długości 8
√2
cm. Oblicz objętość walca.
3. Oblicz stosunek objętości kuli wpisanej w sześcian o danym boku a , do objętości kuli
opisanej na tym sześcianie.
4. Przekrój osiowy stożka jest trójkątem równobocznym o polu równym 15
√5 cm
2. Oblicz pole
całkowite i objętość stożka.
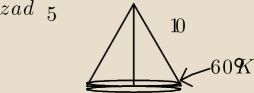
5. Oblicz objętość stożka:
1 gru 16:27

 Przekrój osiowy walca jest kwadratem o boku długości 4. Wyznacz objętość walca.
V=π(4)2 * 4√3
V=π*16*4√3
V=64√3πcm3
l=16
h=4√3
r=4
odp. Objętość stożka wynosi 64√3πcm3
Przekrój osiowy walca jest kwadratem o boku długości 4. Wyznacz objętość walca.
V=π(4)2 * 4√3
V=π*16*4√3
V=64√3πcm3
l=16
h=4√3
r=4
odp. Objętość stożka wynosi 64√3πcm3
 Podstawy trapezu równoramiennego mają dł. 9 i 3 a kąt ostry trapezu ma 60stopni. Oblicz
objętość bryły powstałej w wyniku obrotu tego trapezu do okoła krótszej postawy.
h=9
r=5
V=?
32 +92 = c2
9+81=c2
c2=100
c=10
V=πr2*h
V=π52*9
V=π25*9
V=225π
Powstał walec i dwa stożki złączone podstawami.
Podstawy trapezu równoramiennego mają dł. 9 i 3 a kąt ostry trapezu ma 60stopni. Oblicz
objętość bryły powstałej w wyniku obrotu tego trapezu do okoła krótszej postawy.
h=9
r=5
V=?
32 +92 = c2
9+81=c2
c2=100
c=10
V=πr2*h
V=π52*9
V=π25*9
V=225π
Powstał walec i dwa stożki złączone podstawami.
 zad 2
l = 2r = 6√3
zad 2
l = 2r = 6√3
 zad 4
Pc = πr(r+l) = 48π
l = 3r
πr(r + 3r) = 4πr2 = 48π
r2 = 12
r = 2√3
l = 3r = 6√3
h = √l2 − r2 = √108 − 12 = √96 = 4√6
zad 4
Pc = πr(r+l) = 48π
l = 3r
πr(r + 3r) = 4πr2 = 48π
r2 = 12
r = 2√3
l = 3r = 6√3
h = √l2 − r2 = √108 − 12 = √96 = 4√6
 zad5
h = 18
zad5
h = 18
 1. Wysokość walca jest dwa razy dłuższa od średnicy jego podstawy. Oblicz pole całkowite walca,
jeśli jego objętość wynosi 32π.
2. Po rozwinięciu powierzchni bocznej walca otrzymano kwadrat o przekątnej długości 8√2
cm. Oblicz objętość walca.
3. Oblicz stosunek objętości kuli wpisanej w sześcian o danym boku a , do objętości kuli
opisanej na tym sześcianie.
4. Przekrój osiowy stożka jest trójkątem równobocznym o polu równym 15√5 cm2. Oblicz pole
całkowite i objętość stożka.
5. Oblicz objętość stożka:
1. Wysokość walca jest dwa razy dłuższa od średnicy jego podstawy. Oblicz pole całkowite walca,
jeśli jego objętość wynosi 32π.
2. Po rozwinięciu powierzchni bocznej walca otrzymano kwadrat o przekątnej długości 8√2
cm. Oblicz objętość walca.
3. Oblicz stosunek objętości kuli wpisanej w sześcian o danym boku a , do objętości kuli
opisanej na tym sześcianie.
4. Przekrój osiowy stożka jest trójkątem równobocznym o polu równym 15√5 cm2. Oblicz pole
całkowite i objętość stożka.
5. Oblicz objętość stożka: