ln^{3}x Kasia: obliczyc extremum ln³x . Prosze o pomoc.

M:

Bo_ra: f(x)=ln³(x) f(x)=(ln(x))³

	1
f'(x)= 3ln2(x)*		i x≠0 i x>0
	x

	3ln2(x)
f'(x)=		=0
	x

3ln²(x)=0 ln²(x)=0 x=1

mondrala: brak ekstremum

Bo_ra: A napisz czemu tak? Mnie także sie to przyda

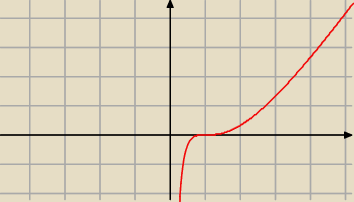
Janek191: W x = 1 funkcja ma punkt przegięcia, bo f '' (1) = 0

Bo_ra: Witam A czemu nie ma ekstremun ? Kazali obliczyc właśnie ekstremum ,a nie punkt przegięcia . Dzięki

Min.Edukacji: Bo caly czas rośnie do ∞

chichi: "W x = 1 funkcja ma punkt przegięcia, bo f '' (1) = 0" rzecz jasna, nie jest to poprawny wniosek

Bo_ra: Dobrze.

Mila: f(x) funkcja różniczkowalna . Zerowanie się pochodnej jest warunkiem koniecznym istnienia ekstremum lokalnego dla funkcji różniczkowalnej, ale nie jest warunkiem wystarczającym. Przy przejściu przez punkt stacjonarny pochodna musi zmieniać znak wtedy f(x) ma ekstremum. 1) f'(1)=0 2) f'(x)>0 dla x<1 i f'(x) dla x>1. (oczywiście dla x∊D_f ) Zatem w x=1 f(x) nie posiada ekstremum. 3) np. f(x)=x³− funkcja różniczkowalna f'(x)=2x² f'(0)=0 warunek konieczny f'(x)>0 dla x<0, f'(x)>0 dla x>0 funkcja nie ma ekstremum w x=0

Bo_ra: Bardzo dziękuje Milu za wytłumaczenie

Min.Edukacji: To teraz tego nie uczą na matmie w 3 klasie?