Element maksymalny i minimalny
Cosik: Element maksymalny i minimalny. Mam problem ze zrozumieniem (począwszy od samej def.)
Max:
"Niech X będzie zbirem uporządkowanym przez relację R
Element a nazywamy elementem maksymalnym zbioru X, gdy a∊X i nie ma w zbiorze X elementów
różnych od a i większych od a."
Min:
"Niech X będzie zbirem uporządkowanym przez relację R
Element a nazywamy elementem maksymalnym zbioru X, gdy a∊X i nie ma w zbiorze X elementów
różnych od a i mniejszych od a."
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Tutaj już pojawiają się moje wątpliwości (w oby def. identyczne).
"nie ma w zbiorze X elementów różnych od a i większych od a."
Dla mnie występuje tutaj sprzeczność, tzn. jeśli nie ma różnych to są identyczne (w moim
rozumowaniu), jeśli są identyczne to automatycznie wyklucza to istnienie większych/mniejszych.
Może ktoś to wyjaśnić?
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Teraz zadanie:
Niech X={3,5,6,10,12}, R={(x,y): x|y}
Wyznaczyć elementy maksymalne i minimalne...
Moje wypociny:
1. Wypisałem wszystkie możliwe przypadki:
R={(3,3), (3,5), (3,6), (3,10), (3, 12), (5,3), (5,5), (5,6), (5,10), (5,12), (6,3), (6,5),
(6,6), (6,10), (6,12), (10,3), (10,5), (10,6), (10,10), (10,12), (12,3), (12,5), (12,6),
(12,10), (12,12)}
2. Następnie sprawdziłem, które x|y
R={(3,3), (3,6), (3, 12), (5,5), (5,10), (6,6), (6,12), (10,10), (12,12)}
3. Z tych elementów wybrałem te, które nie są różne...(większości już nie wiem jak wybrać, bo
skoro są identyczne to nie ma < czy >)
R={(3,3), (5,5), (6,6), (10,10), (12,12)}
I tutaj nie mam już pojęcia co robić... wiem, że maksymalne są to 10 i 12 a minimalne 3 i 5.
Pomoże ktoś zrozumieć?
11 sty 16:48
Cosik: Dodam, że sprawdziłem relację porządku w zbiorze X.
11 sty 17:10
Cosik:
11 sty 17:55
Cosik:
11 sty 18:46
Cosik:
11 sty 18:57
Cosik:
11 sty 19:52
Cosik:
11 sty 20:12
Cosik:
11 sty 20:54
Cosik: pomocy...

11 sty 21:28
Cosik:
11 sty 22:15
Cosik:
11 sty 22:30
Cosik: Jeszcze jeden ref. i się poddaję

11 sty 23:13
Anonimowy: Przybywam, ale zanim co oczyszczę sobie nie co

11 sty 23:17
Cosik: Kurcze, we wtorek poprawkowe kolokwium − muszę to ogarnąć

Zostało mi to i funkcje...

11 sty 23:21
Anonimowy:
Coś się popsuło, dobra tam

Masz złe def.
11 sty 23:23
Anonimowy:
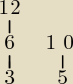
Do takich rzeczy przydaje się diagram Hassego, jak go narysujesz to widzisz co jest elementem
max, a co największych
Element maksymalny to taki, nad którym nie ma innych "rzeczy" , a największy to taki
który jest większy od wszystkich (wtedy jest jednocześnie elementem maksymalnym)
Przykład weźmy Twój: Niech X={3,5,6,10,12}, R={(x,y): x|y}
Robimy diagram: (rys)
Element maksymalny: 12 i 10
Element minimalny: 3 i 5
Element największy i najmniejszy brak
11 sty 23:28
Cosik: Dzięki, do tego diagramu jeszcze nie doszedłem. Widzę jednak, że się on przyda.
Bez diagramu można jakoś łatwo odczytać?
11 sty 23:32
Cosik: Definicje mam z książki "Elementy logiki i teorii mnogości dla Informatyków".
11 sty 23:32
Anonimowy:
Bez diagramu ja się nie uczyłem więc ciężko mi powiedzieć

Ale zauważ, że napisałeś tą samą def. dla obu

11 sty 23:33
Cosik: Poprawka dla min:
Min: "Niech X będzie zbirem uporządkowanym przez relację R Element a nazywamy elementem
minimalnym zbioru X, gdy a∊X i nie ma w zbiorze X elementów różnych od a i mniejszych od a."
11 sty 23:34
Cosik: Dzięki za pomoc, zaraz nauczę się diagramu i chyba wszystko będzie jasne.
11 sty 23:35
Anonimowy: Też tak myślę

Nie ma sensu wkuwać def. trzeba wiedzieć co to oznacza i już
11 sty 23:37
Roberto: To są właśnie fora !
20 cze 16:33



 Zostało mi to i funkcje...
Zostało mi to i funkcje...
 Masz złe def.
Masz złe def.
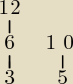 Do takich rzeczy przydaje się diagram Hassego, jak go narysujesz to widzisz co jest elementem
max, a co największych
Element maksymalny to taki, nad którym nie ma innych "rzeczy" , a największy to taki
który jest większy od wszystkich (wtedy jest jednocześnie elementem maksymalnym)
Przykład weźmy Twój: Niech X={3,5,6,10,12}, R={(x,y): x|y}
Robimy diagram: (rys)
Element maksymalny: 12 i 10
Element minimalny: 3 i 5
Element największy i najmniejszy brak
Do takich rzeczy przydaje się diagram Hassego, jak go narysujesz to widzisz co jest elementem
max, a co największych
Element maksymalny to taki, nad którym nie ma innych "rzeczy" , a największy to taki
który jest większy od wszystkich (wtedy jest jednocześnie elementem maksymalnym)
Przykład weźmy Twój: Niech X={3,5,6,10,12}, R={(x,y): x|y}
Robimy diagram: (rys)
Element maksymalny: 12 i 10
Element minimalny: 3 i 5
Element największy i najmniejszy brak
 Ale zauważ, że napisałeś tą samą def. dla obu
Ale zauważ, że napisałeś tą samą def. dla obu
 Nie ma sensu wkuwać def. trzeba wiedzieć co to oznacza i już
Nie ma sensu wkuwać def. trzeba wiedzieć co to oznacza i już