Przebieg funkcji
fler: Znajdź przedziały monotoniczności i ekstrema funkcji
f(x) = 2x3 − 3x2
D ∊ R (bo nie ma mianownika)
f'(x) = 6x2 − 6x = 6x(x−1)
badanie znaku pochodnej
f'(x) > 0 <=> 6x2 − 6x > 0 <=> 6x2 > 6x <=> x > 1
i tu sie zatrzymałem
nie wiem co z tym dalej
11 sty 15:52
Krzysiek:
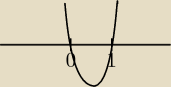
6x(x−1)>0
czyli
x∊(−
∞,0)∪(1,
∞)
11 sty 15:58
fler: no dobrze, ale w takim razie jaka bedzie roznica dla znaku
f'(x) < 0
11 sty 16:07
Krzysiek: a kiedy ten wykres jest pod osią (tzn dla jakich iksów ) ?
11 sty 16:08
fler: no tak, głupie pytania

dzięki
11 sty 16:09
fler: no tylk oteraz tak bo
f'(x) = 0 i wychodzi x = 1
czyli
f↗ dla x ∊ (−∞,0) i (1,∞)
f↘ dla x ∊ (0,1)
f w pkcie x = 1
i teraz rozumiem, że rysuje jakiś inny wykres?
a to, że x = 1 to jest moje ekstremum ?
i nawet jesli tak to nie wiem czy min czy max
11 sty 16:18
fler:
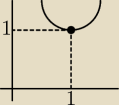
czyli minimum
ten rysunek jest dobrze?
11 sty 16:21
fler: dobra wiem jzu ze nei jest, ale nei wiem jak tozrobic dobrze

11 sty 16:23
fler:
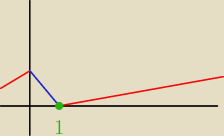
11 sty 16:26
fler: dobra poddaje sie

11 sty 16:33
Krzysiek: przecież z mojego "wykresu" widać, że pochodna zeruje się w dwóch pktach.. dla x=0 i dla x=1
dla x=0
pochodna z lewej strony jest dodatnia z prawej ujemna więc jest to maximum
11 sty 16:36
fler:
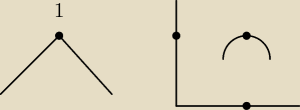
czyl itak?
11 sty 16:49
Krzysiek: ale co tak? nie wiem co to jest..
dla x=1 jest minimum..
(pochodna jest mniejsza od zera potem większa od zera, więc nasza funkcja jest malejąca a potem
rosnąca )
więc w punkcie x=1 jest minimum
11 sty 16:58
 6x(x−1)>0
czyli
x∊(−∞,0)∪(1,∞)
6x(x−1)>0
czyli
x∊(−∞,0)∪(1,∞)
 dzięki
dzięki
 czyli minimum
ten rysunek jest dobrze?
czyli minimum
ten rysunek jest dobrze?



 czyl itak?
czyl itak?