g. analityczna anka: Punkty C=(6,6) i D=(2,4) są krańcami krótszej podstawy trapezu równoramiennego ABCD. Dłuższa podstawa należy do prostej opisanej równaniem y=¹₂x−2. Ramię trapezu ma długość √40 Wyznacz współrzędne wierzchołków A i B.

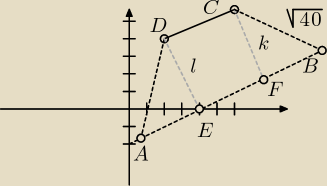
dero2005: oblicz odcinek k (odległość punktu C od prostej AB) oblicz długość odcinka FB z pitagorasa oblicz równanie prostej CF jako prostopadłej do prostej AB i przechodzącej przez punkt C oblicz współrzędne punktu F przez porównanie równan prostych CF i AB oblicz współrzedne punktu B z równania na odległość dwóch punktów F i B punkt A podobnie

anusiak: A(x;1/2x−2) √40 = |AD|=|CB| √40=√(2−x)²+(1/2x−2)² √40=√x²−4x+36−6x+1/4x² | *(²) 40 = 5/4x²−10x+40 5/4x²−40=0 x(x−8)=0 x=0 x=8 y=−2 y=2 Stąd: A(0,−2) B(8,2)

baq: punkt B jest tutaj zle wyznaczony. wartosci przy A sie zgadzaja, ale dla punktu B nalezy tak samo stworzyc drugie, osobne rownanie. dokladnie tak samo jak przy punkcie A. czyli : √40 = √(x−6)² + (x−8)², otrzymujemy rownanie z jedna niewiadoma, wynikiem jest 4 v 12. Z rysunku widac, ze x≠4, czyli punkt B = (12,4)

baq: BŁĄD BŁĄD BŁĄD ! przepraszam. to równanie wygląda tak : √40=√(x_b−6)²+1/2x_b−8)²