pochodne monotoniczność Wojtek: Znaleźć przedziały monotoniczności funkcji. h(x)=e^x(x+1)

ZKS: Policz pierwszą pochodną i zobacz kiedy jest > 0 a kiedy < 0.

Wojtek: (e^x)=e^x ale nic w tym nie widze albo nie zrozumialem

Wojtek: obliczam z twierdzenia h'(x)=(e^x)'*(x+1)+(x+1)'*e^x=e^x(x+1)+e^x co dalej jak uprościć działanie jak 1 pochodna e^x to bedzie >0

ZKS: Przecież masz funkcję e^x(x + 1) a nie e^x.

ZKS: e^x(x + 1) + e^x = e^x(x + 1 + 1) = e^x(x + 2)

Wojtek: to na osi mam zaznaczyc e^x=2.72... czy jakoś tak a drugi x czy pierwiastek −2 ? ale nie bo to nie bedzie parabola prawdopodobnie e to nie wiem

ZKS: e^x dla każdego x ∊ ℛ jest > 0 jako funkcja wykładnicza.

Wojtek: to w takim razie ile wynosi x? bo nie wiem jak narysowac wykres

ZKS: Skoro e^x jest dla każdego x ∊ ℛ > 0 to sprawdzasz tylko x + 2.

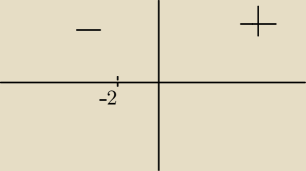
Wojtek: czyli tak bedzie wyglądał wykres czyli f/\ dla argumentów (−2,−1) bo xeR\{−1} ,(−1,∞) f\/ dla argumentów (−∞,−2) czy tak?

ZKS: Rozwiązujesz nierówność h'(x) > 0 ⇔ e^x(x − 2) > 0 ⇒ x − 2 > 0 h'(x) < 0 ⇔ e^x(x − 2) < 0 ⇒ x − 2 < 0

Wojtek: tam powinno byc x+2 nie x−2 h'(x)>0⇔x>−2 h'(x)<0⇔x<−2 czyli dobrzze wykres i monot..