Naszkicuj wykres funkcji (f) określonej w następujący sposób
Joanna: Naszkicuj wykres funkcji (f) określonej w następujący sposób:
5 dla x< −4
x kwadrat + 2x−3 dla −4<x≤2
−x+7 dla 2<x≤5
a) dziedzina i przeciwdziedzina
b) wartość nax. i nim. funkcji
c) maksymalny przedział monotoniczności
d) czy funkcja jest różnowartościowa, uzasadnij
8 sty 00:53
Joanna: tam jest naszkicuj wykres.. ale chodzi mi dardziej o to jak wyliczyć te 3 przykłady tam podane
żeby narysować ten wykres wogóle
8 sty 01:00
Adam:
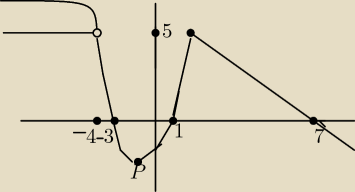
tak wyglad wykres a wyjasniejnie zaraz
8 sty 01:16
Adam: bez tej kteski od lewej strony nad ta pozim=oma od mojego nicku
8 sty 01:17
Adam:
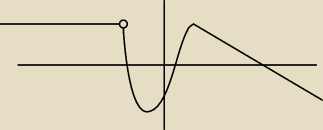
8 sty 01:18
kylo1303: Rysowanie wykresu:
5 dla x< −4
x kwadrat + 2x−3 dla −4<x≤2
−x+7 dla 2<x≤5
1.) W przedziale od −∞ do −4 rysujesz pozioma kreske y=5
2.) f(x)=x2+2x−3 Zaznacz te 3pkt i narysuj parabole ograniczona z obu stron skrajnymi
punktami (x=−4 i x=2)
xw=−1 P1(−1,−4) P2(−4,5) P3(2,5)
3.) masz y=−x+7 P1 (2,5) P2(5,2) − zaznacz te 2 pkt, narysuj odcinek.
8 sty 01:21
kylo1303: Adam Wykres konczy sie na x=5
8 sty 01:21
kylo1303: Ty Joanna wspominalas cos o kolokwium... przeciez to jest poziom gimnazjum...
8 sty 01:22
Joanna: ale kochany jesteś

8 sty 01:22
8 sty 01:23
Joanna: a to a,b,c,d

8 sty 01:23
Adam: wiem ze na 5 sie konczy tylko juz nie mysle a po za tym duzo pochodnych dzi policczyłem i od 13
nad matma siedze
8 sty 01:24
kylo1303: D=(−∞,5>
ZW=<−4,5>
f(max)=5
f(min)=−4
Dla x∊(−∞,−4) funkcja stala
Nie, nie jest roznowartosciowa.
8 sty 01:25
Joanna: ok ok rozumiem

To dobrze że mamy takie spr niż o wiele trudniejsze. Są jeszcze zawodowe a
czasu mało.
8 sty 01:25
Adam: D=(−∞,5) \ {−4}
ZW=(−4,5)
8 sty 01:26
Joanna: DZIĘKUJĘ

8 sty 01:26
Adam: D=(−∞,5> \{4}
8 sty 01:27
Adam: a do d uzasadnienie jest takie ze dla x = −3 i x= 1 funkcja ma takie same wartosci
8 sty 01:28
Adam: i wykres zakoncz rysowac na x=5 ja za daleko poszedlem
8 sty 01:28
kylo1303: Tak samo jak dla x=−100, x=−1000 i dla x=−99999999999

Tak teraz patrze to niby −4 nie nalezy do dziedziny, ale to mogl byc blad w przepisywaniu
przykladu (bo zazwyczaj sie tak nie robi xD )
8 sty 01:29
 tak wyglad wykres a wyjasniejnie zaraz
tak wyglad wykres a wyjasniejnie zaraz



 To dobrze że mamy takie spr niż o wiele trudniejsze. Są jeszcze zawodowe a
czasu mało.
To dobrze że mamy takie spr niż o wiele trudniejsze. Są jeszcze zawodowe a
czasu mało.

 Tak teraz patrze to niby −4 nie nalezy do dziedziny, ale to mogl byc blad w przepisywaniu
przykladu (bo zazwyczaj sie tak nie robi xD )
Tak teraz patrze to niby −4 nie nalezy do dziedziny, ale to mogl byc blad w przepisywaniu
przykladu (bo zazwyczaj sie tak nie robi xD )