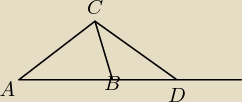
Dowodzenie, trójkąty Help me: W trójkącie ABC przedłużono bok AB poza wierzchołek B i odłożono taki odcinek BD, że |BD| = |BC|. Następnie połączono punkty C i D. Wykaż, że kąt CDA = ¹₂ kątowi CBA. Proszę o jakieś wskazówki i pomoc, gdyż nie mam żądnego pomysłu jak to rozwiązać.

Help me: I jak, ktoś pomoże? Prosiłbym o wskazówki lub objaśnienie od czego mam zacząć, nad czym pomyśleć. Bo to dowodzenie, ale nic do głowy mi nie przychodzi (a wiedzę z geometrii mam, tylko praktyka u mnie siedzi).

Aga: IBDI=IBCI więc trójkąt CBD jest równoramienny, i kat BCD= kątowi BDC=α=kątowi CDA kąt CBD=β=180⁰−2α (suma kątów wewnętrznych w trójkącie wynosi 180⁰) Kąt CBA =γ γ+β=180⁰, bo suma kątów przyległych wynosi 180⁰ γ+180⁰−2α=180⁰ stad γ=2α

	1
α=		γ c.n.u.
	2