funkcja liczbowa: Zbadaj monotoniczność funkcji Gosq: f(x)=−2x² +1 w zbiorze R

emte: policz pochodną, a potem zbadaj jej znak, kiedy jest dodatnia, to funkcja jest rosnąca, a kiedy jest ujemna, to funkcja jest malejąca.

ICSP : Tutaj nawet nie trzeba liczyć pochodnej. To funkcja kwadratowa

gosq: a możesz mi wyjaśnić jak zbadać te przedziały monotoniczności?

Eta:

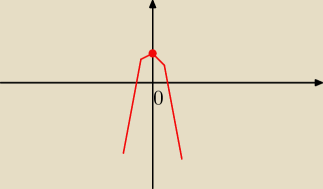
Eta: f(x) ↗ ⇔ x∊(−∞, 0> f(x)↘ ⇔ x∊<0.∞)

gosq: wow, dzięki!

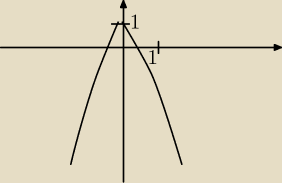
Aga: Robiliście na lekcji z definicji? Na podstawie wykresu.(paraboli) f malejąca dla x∊<0.∞) a rosnąca dla x∊(−∞, 0>

adix: rowiąz −2x² + 1 =0 czyli 1/2=x² i wyliczas te 2 pierwiatki i zanaczasz (wykres będzie skierowany ramionami w dól bo współczynnik przy x² jest ujemny ) i zauwaz ze wykres przecina os OY w punkcie 1 to jest wierzchołek tej paraboli czyli ===> f rosnąca (−OO,1) mALJEJACA (1 ,OO)

adix: sorry.......f rosnąca (−OO,0) mALJEJACA (0 ,OO)

gosq: nie przypominam sobie, nauczycielka powiedziała że mamy sami temat z podręcznikiem przerobić

Aga: Na poziome podstawowym chyba nie wymagają wykazywania z definicji, więc tak jak jest zrobione to wystarczy.