zadanko gosc: W trapezie równoramiennym ABCD, w którym AB || CD oraz AB=2a i CD=a, przekątna AC zawiera się w dwusiecznej kąta DAB. Oblicz długość okręgu wpisanego w trójkąt ABC. Jak wykazać że trójkąt ACD jest równoramienny a trójkąt ABC prostokątny?

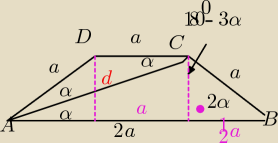
Aga: Kąty naprzemianległe CAB i ACD są równe. z tego wynika, że trójką ACD jest równoramienny.

	P
r=		, P− pole trójkąta ABC, p− połowa obwodu trójkąta ABC.
	p

	0,5a
cos2α=
	a

	1
cos2α=
	2

2α=60⁰ α=30⁰ Ikąta ACBI=180⁰−90⁰=90⁰, więc trójkąt ABC jest prostokątny. d=a√3 r w trójkącie prostokątnym można obliczyć szybciej

	a+2a−d
r=
	2

L=2πr dokończ.

gosc: Dzięki!

gosc: Jak wychodzi ten wzór na promień?

gosc: Bo chciałem innym sposobem to zrobic

gosc: i w sumie to zły wynik wychodzi z tego wzoru

Aga:

	a+2a−a√3		3a−a√3
r=		=
	2		2

odp. L=(3a−a3√3)π A co źle policzyłam? Jaka powinna być odpowiedź?

Aga: chochlik odp. (3a−√3a)π

gosc:

	a(√3−1)
powinno być r=
	2

gosc: a przepraszam zle tam napisałem, długość promienia okręgu, zjadłem słowo

gosc: ale r i tak nie jest to, zrobiłęm innym sposobem, tzn z pitagorasa, więc już ok ale zastanowilo mnie skad wziął sie ten wzor na promien .

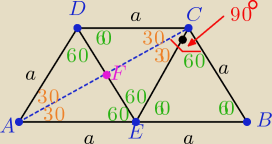
Eta: |AC|= 2*|AF| = a√3 |CB|=a |AB|= 2a długość promienia okręgu wpisanego w trójkąt prostokątny o przyprostokątynych a i b

	a+b −c
i przeciwprostokątnej c wyraża się wzorem: r=
	2

zatem dł. r promienia okręgu wpisanego w ΔABC :

	a√3+a−2a		a√3−a		a(√3−1)
r=		=		=
	2		2		2

Eta:

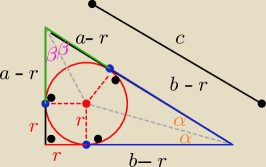
	a+b−c
c= a−r+b−r⇒ 2r= a+b −c ⇒ r=
	2

Aga: Faktycznie , zapisałam źle wzór na r.