Stożek napełniony wodą Pr12: Naczynie w kształcie stożka napełniono do połowy wysokości wodą. Jaką część objętości całego naczynia stanowi objętość wody

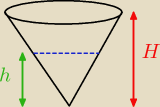
Trivial: Mamy

	1
h =		H
	2

Wystarczy policzyć V_h oraz V_H, a wtedy odpowiedź jest

Vh
	.
VH

Pr12: Skąd pewność, jak jest zorientowany stożek?

Pr12: Ma to jakieś znaczenie od góry czy do dołu − logicznie rzecz biorąc jak będzie stał na podstawie i napełnimy do połowy wysokości to tej wody będzie jednak więcej.

Trivial: Skoro to ma być naczynie, to raczej w drugą stronę ciężko. Aczkolwiek możliwe. Jeśli chcesz, to rozważ dwa przypadki.

Pr12: Tylko właśnie ze wzoru na objętość stożka to nie wynika, bo mam ¹₃SH, więc jak dam h=¹₂ to uzyskuję to samo.

Trivial: Zmienia się także S.

Pr12: Chociaż chyba faktycznie to bez sensu, bo musiałby to być scięty stożek, bo w zasadzie czym jest wierzchołek stożka, gdyby postawić go odwrotnie i chcieć coś za s dać?

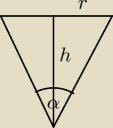
Trivial: Mamy zależność dla stożka

	α		r
tg(		) =
	2		h

Czyli

	α
r = tg(		)*h
	2

Wykorzystamy to w zadaniu.

	α
r = tg(		)*h
	2

	α
R = tg(		)*H
	2

Zatem

	1		1		1		α		1		α
Vh =		hSh =		h*πr2 =		h*π(tg(		)*h)2 =		πtg2(		)h3
	3		3		3		2		3		2

Analogicznie

	1		α
VH =		πtg2(		)H3
	3		2

Czyli:

Vh		1   α   πtg2( )h3 3   2		h		1
	=		= (		)3 =		.
VH		1   α   πtg2( )H3 3   2		H		8

Pr12: Dziękuję, chociaż nadal trudno jest mi sobie wyobrazić wierzchołek idealnego stożka jako okrąg. Czyli tutaj mamy przypadek, że stoi na wierzchołku, ale dla drugiego przypadku tangens połowy kąta nie będzie taki sam?

Trivial: Tangens kąta się nie zmienia, dlatego można uzależnić długość promienia podstawy r od wysokości h. A ten stożek 'stoi' na wierzchołku. Masz odpowiedzi do tego?

Pr12: Nie mam odpowiedzi niestety. W takim razie skoro tangens kąta się nie zmienia to orientując odwrotnie stożek mamy tylko inny rysunek, ale wynik bedzie ten sam?

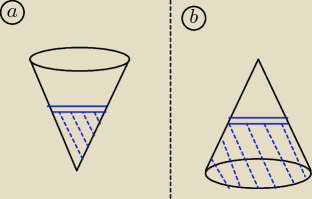
Trivial: Może być dwie sytuacje, chociaż b) jest mi trudno sobie wyobrazić.

	1		1		7
Dla a) wynik to		, dla b) wynik to 1−		=		. Stawiam, że chodziło im o a).
	8		8		8

Pr12: W b było by dokładnie takie samo postępowanie, z tymże później odejmujemy, czyli ogólnie zapamioętac, że skala podobieństwa ze względu na wysokość 1/8 i już pomijamy czy to może tka stać czy nie : P W każdym razie dziękuję