całka powierzchniowa zorientowana gwiazda: hey mam taka prośbę o sprawdzenie lub powiedzenie gdzie błąd robię : ∫∫y²dydx +z³dzdy+ xdxdy , gdzie jest fragmentem powierzchni x²+y²+z²=8zawartym wewnatrz stożka : x=√8−y²−z² liczenie wektora normalnego √8−y²−z² y z

	−y		−z
PO y:		Po z:
	√8−y2−z2		√8−y2−z2

1 0 0 1

	y		z
n= 1,		,
	√8−y2−z2		√8−y2−z2

parametryzacja: y=rsinalfa z=rcosalfa z²+y²+y²+z²=8 podstawiłam za x² wyszło mi , że y²+z²=4 r∊≤0,2≥ alfa≤0,2π≥ x=√8−r² i y i z podstawienie do wektora normalnego. Dobrze to bedzie?

gwiazda: Nie napisałam , że stożek jest x²=y²+z².

Trivial: Jak wygląda pole F?

gwiazda: To jest kula w stożku rysunek

Trivial: No tak, ale jak wygląda pole wektorowe F? Z tej całki nie da się odczytać.

gwiazda: Ale ja Ci napisałam tyle co było:(

Trivial: F = (y², z³, x)?

gwiazda: nie rozumiem , o co Ci chodzi .

Trivial: Z tej całki ∫∫y²dydx +z³dzdy+ xdxdy nie da się odczytać, co trzeba policzyć. Najprawdopodobniej źle przepisana (pomylone dydx).

gwiazda: Możliwe , że pomyliłam ma być dydz, potem dzdx literówka przepraszam

gwiazda: I jak będzie ok całe zadanie oprócz pomylenia pochodnych przepisanych z książki ?

Trivial: Jeżeli 0≤α≤2π, to powinna być parametryzacja y = rcosα z = rsinα. Reszta raczej ok.

gwiazda: Oki super, a mogę się coś spytać?

Trivial: Tylko tam jeszcze chyba trzeba pomnożyć przez jakobian w pewnym momencie. No nie?

Trivial: O co chodzi?

gwiazda: No cała całka jako mnozyć jako jacobian.

gwiazda: Bo mam problem tylko taki że w w jednej czy 2 całkach wyszło mi r<0, 2sinα) i jak wyznaczyć przedział ? wiem to wstyd tego nie umieć

Trivial: przecież wyznaczony. 0≤r≤2sinα. Zmienne zależne.

gwiazda: No wiem , że nie od 0 do 2 π tylko przedział wtedy α? Bo to w innych powierzchniowych. Jak to wyznaczyć sobie.

Trivial: Zależy jaki przykład masz.

gwiazda: to od przykładu zależy ? bo wyszło mi r≤0,2sinα> a w innym r<0,4cosα> i nie wiem jaki kąt ma wtedy przedział.BO podobno to się rysuje te cos i sin ale ja nie wiem jak. bo było x²+y²=2x i podstawiłam i coś takiego wyszło mi , że 2sinα.

Trivial: Trzeba narysować ten okrąg i zobaczyć jak się zmienia α.

gwiazda: To od 0 do π? czy od ^−π₂ do ^π₂? bo ten po x czy po y osi?

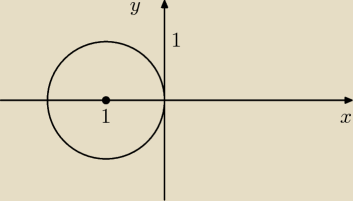
Trivial: Zależy gdzie mierzysz α, ale tutaj to już zobaczysz.

Trivial: Źle narysowałem powinien okrąg być po prawej.

gwiazda: No właśnie też tak myślam bo 1,0 pkt przecież to od 0 do π?

Trivial: Zależy skąd mierzysz α, bo są dwie szkoły. Ja zawsze mierzę od osi x do góry, czyli u mnie

	π		π
przedział byłby [−		,		] (ten okrąg powinien być po prawej).
	2		2

gwiazda: Spoko rozumiem Te zadanie policzyłam do reszty wychodziła całka po r jakaś nie fajna w środku , ale zgadza się , więc biorę się za niezorientowane i koniec a Tobie to nie wiem jak się odwdzięczyć za pomoc wymyśl coś