pola ollla: W równoległoboku o polu równym 120 cm kwadratowych przekątne przecinają się pod kątem 150 stopni. Oblicz długość krótszej przekątnej , jeżeli dłuższa wynosi 16 pierwiastków z 3 cm jest to zadanie z * prosze o pomoc z góry dziękuje

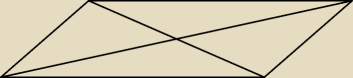
Coma13: Oznaczasz wierzchołki A,B,C,D i środek S, dłuższy bok "a" krótszy "b", krótsza przekątną załóżmy "d"... kąty przecięcia się przekątnych to 150⁰ i 30⁰. > Przekątne dzielą równoległobok na 4 trójkąty.

	d
PBCS =		* 8√3 * sin300
	2

	d
a pole PSCD =		* 8√3 * sin1500
	2

sin150⁰ = sin(90⁰+α) = cos(α) − wzory redukcyjne sin30⁰ = cos60⁰ czyli P_BCS = P_SCD = 2√3d > Równoległobok składa się z 4 trójkątów o równych polach... Tzn że 4*P_SCD = 120cm = 4*2√3d = 8√3d d=120cm / 8√3} = 15 / √3 = 5√3 ....

Coma13: a nie wiem czy jest jakiś sposób żeby nanosić oznaczenia przy obrazku więc sorry jeżeli jest niezrozumiale ale trudno mi się pisze tym "kodem" ;−)