Funkcje madziaa: Okno ma kształt prostokąta zakończonego półkolem jego obwód wynosi 4π m. Znajdź jego wymiary aby przepuszczało jak najwięcej światła? Bardzo proszę o pomoc! Z góry Dzięki!

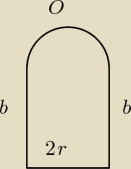
Patronus: Obwód tego okna to: 2b+2r + πr = 4π

	r(−2−π)+4π
b=
	2

Nawięcej światła będzie przepuszczało, kiedy pole będzie największe. Pole to:

	1
b*2r +		* πr2
	2

podstawiając b mamy

	r(−2−π)+4π		1
f(r) =		*2r +		* πr2
	2		2

i trzeba ustalić dla jakiego r ta funkcja przyjmuje największą wartość.

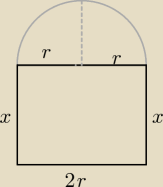Eta: Ob= 2x+2r+πr = 4π ⇒ 2x= 4π−2r −πr

	1
P= 2*x*r+		πr2
	2

	1		1
P(r)= (4π−2r−πr)*r+		πr2 = −2r2−		πr2+4πr
	2		2

	π
P(r)= −(2+		)*r2+4πr −−−− to funkcja kwadratowa, ramiona paraboli do dołu
	2

zatem osiąga max dla odciętej wierzchołka czyli

	−4π		4π
rmax=		=
	π   −2(2+ )   2		4+π

2x= 4π−(2+π)*r

	4π
to 2xmax= 4π−(2+π)*
	4+π

	2π(2+π)		4π
xmax= 2π−		= .................. =
	4+π		4+π

madziaa: Bardzo Dziękuje za pomoc!