rozwiaz rownania i nierownosci iloniek17: rozwiaz równania i nierównosci:

	x +3		4x
a)		=
	2		x−3

	6
b) x +		= 7
	x

	2x +3		6x + 6
c)		=
	3x +2		5x + 4

	x		1
d)		>
	x − 5		2

	x2
e)		≤ 0
	x−1

f) U{(x +1)³ }{(x + 1)² (x − 5) > 0

Krzych:

	(x +1)3
f)		>0
	(x + 1)2(x − 5)

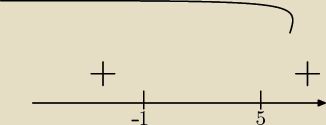
(x +1)³(x + 1)²(x − 5)>0 (x+1)⁵(x−5)>0 x∊(−∞ , −1)∪(5 , +∞)

Krzych: Ojej, nie wiem czemu wstawiło się takie koślawe gówno. W podglądzie jak wysowałem wyglądało ładnie.

Krzych:

	x2
e)		≤0
	x−1

x²(x−1)≤0 x∊<0 , 1>

Krzych: A przepraszam, x∊<0 , 1) bo w mianowniku jest x−1 a musisz założyć, że mianownik jest różny od zera

krystek:

	1
@KrzychA wstaw za x=−		i nierównośc bedzie spełniona .Więc jak?
	2

Drugie pytanie Czy x może być równe 1? Pomyśl!

Krzych: A co do pozostałych zadań to spróbuj sam. Ogólna zasada postępowania z równaniami i nierównościami wymiernymi jest taka: 1. Zakładasz, że wszystkie mianowniki są różne od zera 2. Przenosisz wszystko na jedną stronę 3. Sprowadzasz do wpsólnego mianownika 4. W równaniach piszesz układ równań. Jedno równanie to licznik równa się zero, a drugie to mianownik jest różny od zera. 4. W nierównościach przemnażasz licznik przez mianownik i rysujesz wykres otrzymanego wielomianu i z niego odczytujesz odpowiedź.

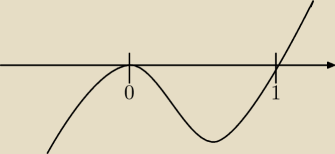
Krzych: Że x nie może być równy 1 to już zdążyłem zauważyć zanim napisałeś swojego posta. A co do tego drugiego to masz racje, kiedy pierwiastek jest parzystego stopnia to wykres "odbija" od osi a nie przecina jej. Robiłem szybko bo zobaczyłem, że zadanie proste i wkradł mi się taki błąd przez nieuwagę. Wykres powinien wyglądać tak, zatem x∊(−∞ , 1)

iloniek17: ślicznie dziekuje

krystek:

iloniek17: przykład d będzie wyliczony z delty? bo nie jestem pewna czy dobrze mi wychodzi

Krzych: Żeby się zrehabilitować zrobię jeszcze podpunkt c, bo wygląda na najbardziej żmudny.

2x+3		6x+6
	=
3x+2		5x+4

3x+2≠0 ⇒ x≠−²₃ ∧ 5x+4≠0 ⇒ x≠−⁴₅

2x+3		6x+6
	−		=0
3x+2		5x+4

(2x+3)(5x+4)−(6x+6)(3x+2)
	=0
(3x+2)(5x+4)

(10x2+23x+12)−(18x2+30x+12)
	=0
(3x+2)(5x+4)

10x2−18x2+23x−30x+12−12
	=0
(3x+2)(5x+4)

−8x2−7x
	=0
(3x+2)(5x+4)

−8x²−7x=0 8x²+7x=0 x(8x+7)=0 8x(x+⁷₈)=0 x(x+⁷₈)=0 x=0 ∨ x=−⁷₈

Krzych:

x		1
	>
x−5		2

x−5≠0 ⇒ x≠5

x		1
	−		>0
x−5		2

2x		x−5
	−		>0
2(x−5)		2(x−5)

krystek:

	x		1
masz		−		>0
	x−5		2

2x−1(x−5)
	>0
2*(x−5)

x+5
	>0 i teraz masz m zerowe x=−5 lub x=5
2(x−5)

Parabola z gałęziami do góry i x∊(−∞,−5)U(5,∞)

Krzych: Ach, przypadkiem wysłałem, chciałm kliknąć powrót do edycji, już robię dalej.

Krzych: O, no to już nie muszę robić dalej. Poprawne rozwiązanie jest dokładnie takie jak przedstawił krystek

iloniek17: a mam pytanie co do przykladu c, dlaczego zostal zmieniony znak? −8x2−7x=0 8x2+7x=0

krystek: Mnozysz obustronnie przez (−1)

iloniek17: ok, w przykładzie b wynikiem jest: 7x (x+12) = 0 x=0 ∨ x= 12 ?

krystek: nie!

krystek: x²−7x+6=0 x≠0 Δ= ...x₁=..x₂=...

iloniek17:

	6
x +		= 7
	x

	6
x +		+ −7 =0
	x

x		6		7
	+		+		= 0
x		x		7

x *x *7 + 6*x*7 + 7*6*x
	= 0
2x +7

7x2 + 42x + 42x
	=0
2x +7

7x2 = 84x
	=0
2x +7

7x² +84x =0 x(7x +84) = 0 7x (x +12) =0 x=0 ∨ x = 12 to moje rozwiazanie, gdzie jest błąd?

iloniek17: w przykladzie a jest x² +6x − 9 = 0? i z tego delte wyliczyc?

Krzych: Jest PEŁNO błędów: w trzeciej linijce:

	x		x2
1) x≠		lecz x=
	x		x

	7		7x
2) −7≠		lecz −7=−
	7		x

w czwartej linijce: 3) jak dodajesz ułamki to muszą mieć wspólny mianownik i dodajesz wtedy tylko liczniki a nie mianowniki ¹₂+¹₃ to ⁵₆ a nie ²₅

Krzych: x+⁶_x=7 x≠0 x+⁶_x−7=0 {x²}{x}+⁶_x−^7x_x=0 Ponieważ to jest równanie, a nie nierówność i założyliśmy już, że x≠0 to możemy obustronnie przemnożyć przez x i otrzymamy: x²−7x+6=0 (x−1)(x−6)=0 x=1 ∨ x=6

iloniek17: faktycznie... racja..

iloniek17: a w przykladzie a wyjdzie x² + 8x − 9 = 0 i z tego jak wyliczyłam x1 = −9 a x2 = 1?