Oblicz pole obszaru ograniczonego Edzio: Oblicz pole obszaru ograniczonego wykresami funkcji:

	1
y=|x−2|+1 i y=|(		)x−1|+3
	2

Nie wiem jak się do tego zabrać, a wpisując treść zadania w google wyskakują zadania z całkami − a to zadanie z liceum.

Krzysiek: narysuj sobie te funkcje i przedziel prostą x=2 na dwa obszary (dwa jednakowe) i policz jeden z nich np. przyjmując za podstawę bok: A=(2,0) i B=(2,3)

-:): ... to rysuj wykresy ... nakładaj ... i licz pola trójkątów ...−

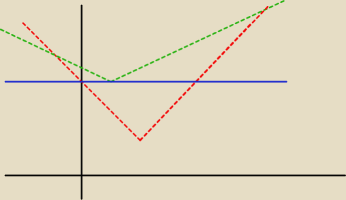
-:): Krzysiek .... a to nie będzie tak?

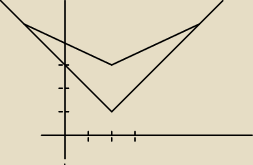
Krzysiek: punkty przecięcia to: (−2,5),(6,5) tylko że tam błędnie podstawę napisałem jeden z punktów to A=(2,1)

Edzio: A jak obliczyć pole tego trójkąta (po podziale)? I jeszcze jeden przykład, w którym dziwny wykres mi wychodzi: y=|2x|−2 i y =|x−1|+1

Edzio: Do przykładu który napisałem powyżej znalazłem takie rozwiązanie: A=(2,2) B=(−4,6) oraz wierzchołki wykresów C=(0,−2) i D=(1,1) obszar między nimi to czworokąt ADBC rozbijam na ΔADC i ΔBDC P=1/2 W(CD,CA)+ 1/2W(CD,CB)=1/2W([1,3],[2,4])+1/2W(1,3],[−4,8])= 1/2I4−6I+1/2I8+12I=1+10=11 Może ktoś napisać co to za wzór powyżej ?

Edzio: Znalazłem, jest to wzór z metody wyznacznikowej