;/ KASIA. : pomocy ! Wyznacz współczynnik p i q funkcji kwadratowej f(x) =x²+px+q, wiedząc że jej wykres jest symetryczny względem prostej x=2 oraz,m że f(4) = 3 będę wdzięczna za wytłumaczenie

Krzych: Jeżeli wykres jest symetryczny względem prostej x=2 to wiemy, że odcięta (pierwsza współrzędna) wierzchołka tej funkcji to 2 ponieważ wykresem funkcji kwadratowej jest parabola. Zapiszmy równanie tej funkcji w postaci kanonicznej: y=(x−2)²+c gdzie c jest rzędną (drugą współrzędną wierzchołka) Teraz ułóżmy równanie korzystając z tego, że wiemy iż f(4)=3 3=(4−2)²+c 3=2²+c c=3−4 c=−1 zatem nasze równanie w postaci kanonicznej wygląda następująco: y=(x−2)²−1 Teraz przekształcimy nasze równanie do postaci ogólnej aby znaleść współczynniki p i q y=(x−2)²−1 y=x²−4x+4−1 y=x²−4x+3 Teraz pięknie widać, że skoro x²+px+q=x²−4x+3 to p=−4 zaś q=3

Krzych: Wytłumaczyłem dostatecznie dobrze?

krystek: bardzo dobrze ,tylko zainteresowana nie odpowiada.

KASIA. : tak b. dziękuje a mam jeszcze takie... dana jest f.kwadratowa f(x) =−x² +5x+6 , wyznacz zbiór argumentów, dla których funkcja przyjmuje wartości ujemne oraz dodatnie.

bartek: no to najpierw policz delte i podaj mi wyniki miejsc zerowych (x1, x2)

KASIA. : 6 i −1

krystek: Wykres ,gałęzie w dół i zobacz dla jakich x masz dodatnie wartości(nad osia OX) a dla jakich ujemne(pod osia OX) Podaj ile wynosi wg Ciebie Δ?

bartek: skoro wyraz a w delcie jest ujemny to "parabolka smutna" czyli ramionami w dól na ukladzie wspolrzednych. podaj przedział dodatni i ujemny funkcji kolezanko

bartek: a tak na marginesie postanowilem sprawdzic Δ i u mnie jest x1 = 1, x2 = −6 a ty podałas −1 i 6.

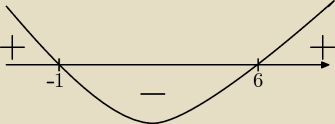
Krzych: −x²+5x+6<0 −x²+5x+6>0 x²−5x−6>0 x²−5x−6<0 (x−6)(x+1)>0 (x−6)(x+1)<0

KASIA. : nie, miejca zerowe na pewno sa dobrze −1 i 6 a delta wynosi 49 więc √Δ = 7

bartek: −5−7 przez 2 to −12:2= −6 −5+7 przez 2 to 2:2 = 1 Wzór ma −b − √Δ przez dwa oraz −b + √Δ

KASIA. : jest −5−7 przez −2 a nie 2

Krzych: Δ=b²−4ac Δ=5²−4*(−1)*6 Δ=25−(−24) Δ=25+24 Δ=49 √Δ=√49 √Δ=7

	−b−√Δ
x1=
	2a

	−5−7
x1=
	2*(−1)

	−12
x1=
	−2

x₁=6

	−b+√Δ
x2=
	2a

	−5+7
x2=
	2*(−1)

	2
x2=
	−2

x₂=−1 Oj panowie, chybe nie umiecie liczyć

KASIA. : no

bartek: ja pier.....zapomniałem o tym 2a. jeszcze nie odespalem sylwestra, ide stad bo ludzi w blad wprowadzam

krystek: Ale gałezie w dół!

KASIA. : no dobra to to wiem.. i jak teraz ma być że : w. ujemne (−1,6 ) w. dodatnie (−∞,−1)∪(6,+∞)

Krzych: Kochanie, weź sobie to spróbuj rozwiązać algebraicznie, co? Nauważ, że napisałem nierówność i przemnożyłem ją przez −1, żeby łatwiej było mi skorzystać z wzorów Viète'a i żebym nie musiał liczyć delty. Próbowałeś kiedyś rozwiązywać funkcję kwadratową algebraicznie czy zawsze robicz to graficznie?

krystek: Odwrotnie!

Krzych: Gdybym odwrotnie narysował parabolę (co krystek mi zarzuca) to powinien wyjść mi zły wynik. A wyszedł dobry. I ładniej będzie wyglądało jak napiszesz: f(x)<0 dla x∊(−1,6 ) f(x)>0 dla x∊(−∞,−1)∪(6,+∞) Twoja matematyczka bardziej się ucieszy

KASIA. : a czemu odwrotnie ? nie wiem ; /

Krzych: Fakt, odwrotnie, bo −x²+5x+6<0 gdy (x−6)(x+1)>0 a mój wykres narysowałem dla (x−6)(x+1) a nie dla −x²+5x+6

KASIA. : to ja mam w koncu dobrze czy nie ?

krystek: Krzychu ,nie wprowadzaj Kasi w bład!

krystek: @Krzychnierówności kwadratowe i wyższych stopni rozwiazujemy graficznie!

Krzych: f(x)>0 dla x∊(−1,6 ) f(x)<0 dla x∊(−∞,−1)∪(6,+∞) ZROZUMCIE, ŻE −x²+5x+6<0 gdy (x−6)(x+1)>0 A MÓJ WYKRES POGLĄDOWY JEST DLA (x−6)(x+1) A NIE DLA −x²+5x+6 I nie wprowadzam nikogo w błąd, mały chochlik może się wkraść każdemu. Po prostu rozwiązuję zadanie algebraicznie a nie graficznie, rozumiesz, czy to dla Ciebie za ciężkie?

Krzych: @krystek na jakim poziomie edukacji? Zresztą narysowanie uproszczonej paraboli tudzeż wykresu wielomianowego to jeszcze nie rozwiązanie graficzne. A trzeba wszystko najpierw policzyć.

Krzych: I jak masz pytanie dla jakich wartości wielomian dajmy na to szóstego stopnia przyjmuje wartości ujemne to będziesz rysował jego wykres czy najpierw doprowadzisz do postaci iloczynowej a potem narysujesz uproszczony i z niego odczytasz?

KASIA. : dobra chłopaki spokojnie : )) to w końcu który am racje ? ; )

krystek: przecież ,to wszystko wiadomo, o czym dyskutujemy? Przeczytaj uważnie co napisałeś o 20:19!

KASIA. : w. ujemne (−∞,−1)∪(6,+∞) w. dodatnie (−1,6 ) takma byc ?

Krzych: W końcu obaj, bo tak na prawdę mówimy o tym samym tylko minimalnie inczej to nazywamy

KASIA. : ok dzięki : ] aa jeszcze jedno, ostatnie pytanie jeśli mam x² = −3 to jest sprzeczne równanie prawda czy nie ?

Krzych: tak, bo każda liczba rzeczywista podniesiona do kwadratu jest większa bądź równa 0

KASIA. : czyli dalej nie mogę tego pierwiastkować i po prostu rozwiązania nie ma ?

Krzych: Tak. Liczba podpierwiastkowa nie może być ujemna. Jak na przykład pojawia Ci się gdzieś w zadaniu √x−3 to musisz napisać założenie x≥3 bo dla x<3 równanie nie ma sensu liczbowego. Oczywiście jeżeli rozmawiamy o zbiorze liczb rzeczywistych, bo kiedy urojone wchodzą do gry to jest już całkiem co innego i sprawa mocno się komplikuje, ale tym będziesz się martwić dopiero na studiach.

Bartek: Zazwyczaj pytam, więc tym razem dorzucę się do podpowiedzi. Wyrazenie x² +3 zawsze jest ≠0 i zawsze jest dodatnie. Słuchajcie, jak się czyta wasze odpowiedzi, to się można ze śmiechu popłakać. Serio! Jeden kabaret − pozytywnie oczywiście.

Krzych: rozwiązaniem równania x²=−3 jest x∊∅ czyli inaczej mówiąc równanie to jest sprzeczne, tudzież nie ma rozwiązania.