funkcja
outsider: jak wyznaczyć asymptoty funkcji homograficznej

2 sty 21:59
2 sty 22:03
outsider:
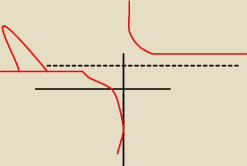
czyli asymptote pionową ma w 0, a pozioma w 2

2 sty 22:08
outsider: czy można zapisać w takiej postaci wzór
2 sty 22:21
beti: nie
| | x2+1 | |
po sprowadzeniu do wspólnego mianownika będziesz miał |
| więc czy to jest na pewno |
| | x | |
dobry przykład?
2 sty 22:35
outsider: czyli do jakiej postaci to doprowadzić, żeby było łatwo wyznaczyć asypmtoty tej funkcji

2 sty 22:40
outsider: | | 1 | |
f(x)=x+ |
| jak z tego wyznaczyc asymptoty? |
| | x | |
2 sty 23:04
beti: wydaje mi się, że ta funkcja ma as. pionową x=0 i jakąś as. poziomą. Ale głowy za to nie dam
2 sty 23:13
beti: znaczy ukośną chciałam napisać

2 sty 23:14
beti: tak, as. ukośna jest i ma równanie y=x
2 sty 23:28
outsider: czyli mam funkcję liniową narysować, oraz hiperbolę
2 sty 23:30
Adi: Asymptota pionowa istnieje tylko kiedy wyrzycasz coś z dziedziny (w tym przypadku 0).
Nie ma asymptot poziomych.
Asymptota ukośna: a=lim{(x2 +1)\x2)=1
b=lim[x−1\x −x]=0
Asymptota ukośna y=x
2 sty 23:30
beti: Nieee, wykresem nie jest hiperbola tylko krzywa, której dwie części zawarte są pomiędzy
asymptotami x=0 i y=x. Wyznacz sobie kilka punktów i zaznacz je w ukł. wsp. to sam zobaczysz.
2 sty 23:33
outsider:
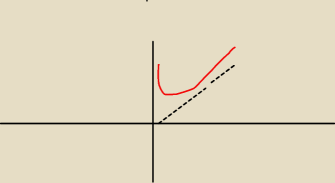
czyli coś takiego ma powstaĆ
2 sty 23:45
Adi:
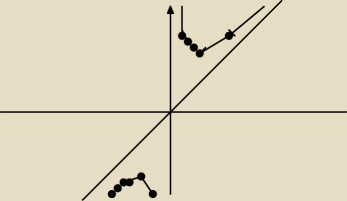
rysunek brzydki ale zarys jesti ta funkcja tak zbliza sie do y=x i x=0
2 sty 23:51
outsider: a jeżeli mam narysować ją na przedziale (0,1), to tylko to co na górze jest i tylko część tej
krzywej
2 sty 23:54
Adi:
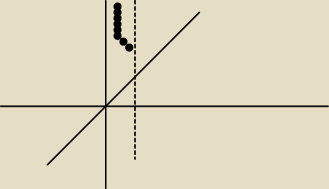
y
2 sty 23:56
outsider: wielkie dzięki, za tak ogromne poświęcenie

2 sty 23:59

 czyli asymptote pionową ma w 0, a pozioma w 2
czyli asymptote pionową ma w 0, a pozioma w 2


 czyli coś takiego ma powstaĆ
czyli coś takiego ma powstaĆ
 rysunek brzydki ale zarys jesti ta funkcja tak zbliza sie do y=x i x=0
rysunek brzydki ale zarys jesti ta funkcja tak zbliza sie do y=x i x=0
 y
y
