funkcja wymierna Bartek: http://www.zadania.info/d29/665840 Przepraszam, ale tak jak rozumiem, że mianownik nie może mieć tutaj miejsc zerowych, tak za diabły nie trafia do mnie ich tłumaczenie. Rozumiem, że dziedzina t∊<0;+∞),bo t=x². Rozumiem, że jeśli t=0, to mam m²≥0, ale po co oni wyskakują z tym nie ujemnym pierwiastkiem, skoro chodzi o to, że mianownik ma po prostu tych pierwiastków nie mieć.. Przecież współczynnik przy t² może być ujemny. Parabola nie może tylko przecinać osi oX. Wydawało mi się, że funkcja kwadratowa może nie mieć pierwiastków przy a<0.

ZKS: Ale skoro współczynnik przy t² będzie ujemny to i to równanie będzie miało miejsce zerowe.

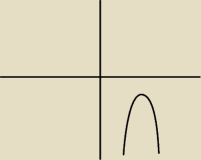
Bartek: O, dzięki.Wiesz, też mi to przyszło do głowy, ale z drugiej strony wydawało mi się, ze może być też taka sytutacja: a<0 i też nie ma miejsc zerowych.

Bartek: No dobrze, rozumiem. Jeżeli m+2<0, to wtedy tak czy siak będą miejsca zerowe,bo na końcu jest m². No tak, rozumiem. Jednak, nie wiem jak ty, ale dla mnie myląca jest informacja o nieujemnym pierwiastku, skoro chodzi o to, że ma ich w ogóle nie być.

Bartek: Nie. Przejrzałem to wszystko jeszcze raz i nie mogę tego ogarnąć. Najpierw piszą, że m≠−2. Potem w odpowiedzi piszą: <−2;.... Jeśli ktoś ma czas i ochotę, to chętnie poproszę o wytłumaczenie tego, bo oni stosują za dużo skrótów myślowych, za którymi ja artysta po prostu nie nadążam.

ZKS: Oczywiście że sytuacja taka może być. Ale na Twoim rysunku widzimy że Δ < 0 i a < 0 a w zadaniu jeżeli a < 0 to Δ > 0 i wtedy nie mieli byśmy pierwiastków nieujemnych.

ZKS: Najpierw jest napisane że dla m = 2 trzeba sprawdzić co się stanie z równaniem dwukwadratowym a jak się okazuje dla m = 2 dziedziną są wszystkie liczby rzeczywiste. Natomiast później trzeba założyć że m ≠ 2 bo sprawdzamy teraz równanie dwukwadratowe.

Bartek: No zaczynam łapać, ale jakieś straszne głupoty mi wychodzą gdy na piechotę chce sprawdzić przypadek, gdy a<0: Δ=44m² + 144m +144 + 4m³. I nie wiem teraz, czy mam obliczyć z tego następną deltę i sprawdzić czy jest faktycznie >0 ? Tylko, że chyba nie istnieje coś takiego jak delta z wielomianu 3 potęgi ....i w ogóle delta z wielomianu

ZKS: Jest Δ z wielomianu stopnia 3 tylko że strasznie nie przyjemna. Tutaj są wykorzystane wzory Viete'a w tym zadaniu t₁t₂ < 0 ⇒ (t₁ > 0 ∧ t₂ < 0) ∨ (t₁ < 0 ∧ t₂ > 0). Czyli jeżeli a < 0 to równanie będzie miało dodatni jeden pierwiastek bo c jest zawsze ≥ 0.

Bartek: Rany julek....wzory...Viete'a. Że też o nich zapomniałęm. Jak na nie spojrzałem, to faktycznie...skoro c jest ≥0, to przy a<0 musi być ujemny jeden z pierwiastków. Ale też tutaj nie chwytam jednej rzeczy. Ok, c≥0. Jednak skoro chcemy uniknąć liczenia delty, to przecież ze wzoru x1x2=c/a nie wynika, że Δ<0. Jak więc przy pomocy wzorów Viete'a wyciągnąć wniosek, że przy m+2>0 nasza Δ<0 ? A może wynika, tylko jestem ślepy.

Bartek: Tak w ogóle, to jeszcze próbuje dorzucić tę informacje o pierwszej współrzędnej wierzchołka. Co ona mi tak na prawdę daje, skoro i tak potrzebuje y wierzchołka .Po podstawieniu −3 i tak mam przecież zamiast konkretnej liczby funkcję. Chyba, że chodzi tu o zbadanie kiedy (po podstawieniu mojej −3) otrzymana funkcja jest dodatnia. Czy ja dobrze kombinuję

ZKS: Ze wzoru na Δ po prostu Δ = b² − 4ac więc jeżeli a < 0 (wiemy że c ≥ 0 dla każdego m ∊ ℛ) ⇒ Δ = b² + 4ac dlatego Δ > 0.

Bartek: Okej, rozjaśniło mi się, tak, okej już rozumiem. Jakie to się proste teraz wydaje. A jeszcze odnośnie Δ=0. Czy aby wykluczyć Δ=0, muszę wykonać te wszystkie obliczenia? Bo jeżeli c≥0, to Δ może być równa zero jedynie wtedy gdy b=0 i faktycznie c=0. To, co napisałeś jest super i spoko łapię. Jednak w ten sposób omijam właśnie Δ=0.

Bartek: Nie jestem urodzonym matematykiem. To da się zauważyć

ZKS: Jeżeli b = 0 to automatycznie a = 0 (zauważ czemu?) więc wtedy byśmy nie rozpatrywali funkcji dwukwadratowej.

Bartek: A....jołki dołki...he Znaczy...to faktycznie widać, przy a i b =0. Ale jeśli mam a>0, to mamy wtedy: Δ=b² − 4ac, czyli klasyczną postać delty. Jak więc zbadać Δ=0 przy a>0 ? Czy wtedy muszę zbadać wilomian: [6(m+2)]² − 4(m+2)m² =0 ? Zaraz, przecież to się zeruje gdy m=−2. Swietnie, dlaczego więc oni uwzględnili m=−2 w odpowiedzi, skoro przy m=−2 Δ=0. Prawdę mówiąc zastanawia mnie czy to się wzajemnie nie gryzie. Oni piszą, że przy m=−2 mamy w mianowniku 4 (funkcja stała). To dlaczego przy m=−2 delta robi mi się =0 ? Przecież funkcja stała to funkcja stała, a jeżeli mam Δ=0, to wychodzi chaos.

ZKS: Nie wychodzi żaden chaos. Na początku sprawdzamy kiedy funkcja f(t) = (m + 2)t² + 6(m + 2)t+ m² nie jest funkcją dwukwadratową czyli dla a = 0. Widzimy że dla m = −2 współczynnik a = 0 b = 0 i c = 4 czyli dla m = −2 dziedziną są wszystkie liczby rzeczywiste bo 4 nigdy nie przetnie osi OX. Później jednak należy założyć że m ≠ 2 bo teraz sprawdzamy funkcję dwukwadratową. Ale w końcowej odpowiedzi trzeba dodać m = −2 bo spełnia polecenie zadania. Rozumiesz?

Bartek: Jest niestety jedna rzecz, której nie rozumiem (niestety, sory). Co więc (abstrahując od tego zadania) oznacza tak na prawdę informacja Δ=0 ? Zazwczyczaj oznacza ona, że mamy jeden pierwiastek i zazwyczaj Δ=0 nie oznacza funkcji stałej. A w naszym przypadku, przy tym diabelnym m=−2, które daje nam funkcję stałą 4 − jeśli mimo wszystko (może z głupoty) zastosuje, przy tym m=−2, wzór na deltę − wychodzi wniosek, że nie jest to funkcja stała y=4 tylko funkcja o jednym pierwiastku. To, co napisałeś jest git i widzę już o co chodzi.

ZKS: Dla m = −2 mamy funkcję stałą y = 4. Później stosujemy założenie że m ≠ 2 bo chcemy rozpatrywać równanie dwukwadratowe. Powiedz jeżeli dalej tego nie rozumiesz.

Bartek: Rozumiem. Dla m=−2 funkcja stała y = 4 a dla m≠−2 funkcja dwukwadratowa. Hip hip. Hura! Wiem. Masz ochotę napisać:"Jupiii..." NIe, ale tak już na serio to dzięki wielkie. Kto inny by mi napisał: "wracaj matole do szkoły i tyle".

ZKS: Wracaj matole do szkoły i tyle. Oczywiście żartuję nie wszystko jest oczywiste od razu trzeba chwilę się zastanowić więc ja się cieszę że potrafiłem wytłumaczyć to Tobie.

betibr: https://matematykaszkolna.pl/forum/119161.html pomocy!