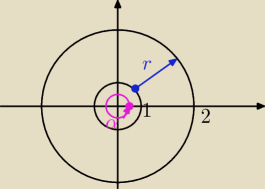
całki podwójne=współrzedne biegunowe gwiazda: ∫∫xydxdy 1≤x²+y²≤4 x=rcosalfa y=rsinalfa r≤1,2≥ Jacobian r a jak wyznaczyc alfe ? Bo rozwiazanie calki to wiem jak.

Krzysiek: alfa od 0 do 2π, ale r jest od 0 do 2

gwiazda: a czemu od 0 ? jak jest od 1 do 4 ?

Krzysiek: mój błąd nie zauważyłem tej jedynki

gwiazda: No właśnie to na pewno od 0 do 2πwtedy przedzial?

Trivial:

gwiazda: Dzięki Trivial Mogę się coś spytac z potrojnych, jeśli masz chwilkę ? bo podwojne zrobiłam już biegunowe wszystkie sobie z reszta problemu nie miałam

Trivial: Napisz, ale będę za 30 min.

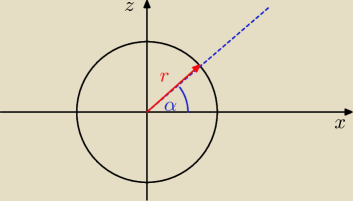
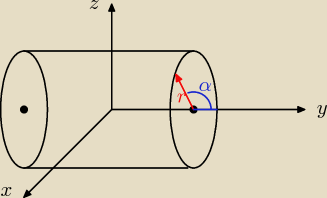
gwiazda: To tak , bo potrójne ani jednej na ćw nie było , a na kolosie będzie norma. Bo mam pytanie do 2 całek , żeby miec pojęcie jak zaczac. 1)∫∫∫ (x²+y²+z)dxdydz gdzie jest walcem o równaniu (x,y,z)∊R³ x²+y²≤4 −1≤z≤1 wiec x=rcosalfa y=rsinalfa z=2? r≤0,2≥ alfa≤0,2π≥ z≤−1,1≥ Jacobian=r tak? Bo obliczyć całkę to nie ma problemu już. 2) ∫∫∫xdxdydz gdzie jest walcem x²+z²≤8 0≤y≤2 wiec wyliczam z=√8−x² x=rsinalfa Jacobian=r Przedziały y mam, 0≤z<√8−x² i co z x? tak?

Trivial: 1) Co to za z = 2? z = z. Reszta dobrze, pod całką wyjdzie (r²+z)r drdrφdz. 2) Podobnie jak poprzednio, ale zrobiłbym inne podstawienie. Ta bryła to obrócony walec (zamiast wzdłuż osi z, 'idzie' wzdłuż osi y). x = rcosφ y = y z = rsinφ 0 ≤ r ≤ 2√2 0 ≤ y ≤ 2. Jakobian pewnie r.

Trivial:

Trivial:

gwiazda: A z bedzie w 2 takie jak napisalam?

Trivial: Byłoby OK, ale długo będziesz potem liczyć. Z podstawieniem 'odwróconym biegunowym' całka sprowadza się do policzenia całki z r² i cosφ (oddzielnie).

Trivial: 0 ≤ z ≤ √8−x².

Trivial: −√8−x² ≤ z ≤ √8−x² sorry.

Trivial: Granice bez zamiany na biegunowe wyglądałyby tak: −2√2 ≤ x ≤ 2√2 −√8−x² ≤ z ≤ √8−x² 0 ≤ y ≤ 2.

gwiazda: Oki rozumiem , liczyłam sobie z współrzednych inna to mi wychodzi i eliptycznymi tez powinnam dac radę tylko najgorsze są inne jak z=....Dziękuje za pomoc

Trivial: Proszę.

gwiazda: I mam pytanie jeszcze jedno z=0 z=3−x²+y² x²+y²=3 i będę mieć r(0,√3) alfa(0,2π) z(0,3−x²−y²)?

Trivial: z = 3−x²+y² czy z = 3−x²−y²?

gwiazda: z=3−x²−y², 1 wyszło zadanie

Trivial: Granice wyjdą takie jak podałaś, z tym że z ∊ [0, 3−r²].

Trivial: I na kolosie radzę dużo rysować.

gwiazda: A rysunki wiem Ale rysunki na forum to mi schodza a na kolosie moge nie zdac go , bo zdałam krzywoliniowe ale do egzaminu sie ucze i przy okazji do kolosa To dziś dziękuję za pomoc porobię reszte co wiem i starszy mi dziękuje Ci i za czas poswiecony

Trivial: Powodzenia na kolosie.

gwiazda: Nie dziekuje i jeszcze powierzchniowe , ale mam czas troche by sie nauczyc tydzien