ZAD elizabeth : w trójkącie równoramiennym ABC, w którym |AC| =|BC| i kąt ACB = α poprowadzono dwusieczną kąta CAB przecinającą bok BC w punkcie D . wiedząc, że |AD| =|AB|=|CD| : a) wykaż, że trójkąty ABC i BDA są podobne b) oblicz miarę kąta α między ramionami trójkąta ABC

Eta: Zostawiam dla Godzia lub ICSP

Godzio: Ja zostawiam dla ICSP

Eta: a feee

Godzio: ICSP ma planimetrie, jemu się przyda a mi nie hehe

Eta: To zbyt proste

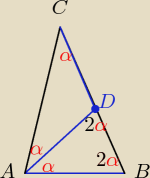
Eta: a) ΔABC jest równoramienny o kącie między ramionami α ΔABD jest równoramienny też o kącie między ramionami α zatem: ΔABC ~ ΔBAD z cechy (b,k,b) b) α+2α+2α= 180^o ⇒ 5α=180^o ⇒ α= 36^o