prosze o pomoc :(( mariolka: Punkt P=(3,4) jest wierzchołkiem równoległoboku , którego jeden bok lezy na prostej y=x , a drugi na prostej y=1/2 x + 1 . Oblicz pole tego równoległoboku.

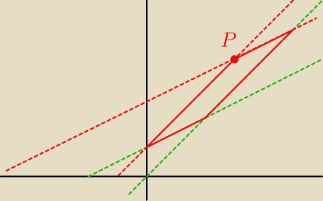
-:): Punkt P nie spełnia równań tych prostych nie leży więc na nich Przez ten punkt piszesz równania prostych równoległych do tych danych Odnajdujesz pozostałe wierzchołki ....itd −

mariolka: tylko własnie ja kompletnie nie mam pojecia jak to dalej robic

-:): prosta y=x ma współczynnik kierunkowy ? prosta równoległa do niej ma współczynnik kierunkowy ? ... a dodatkowo ma przechodzić przez P prosta y=¹₂x+1 ma spóczynni kierunkowy ? prosta równoległa do niej .. itd −

-:): mariolka vel fejsbukowicz −

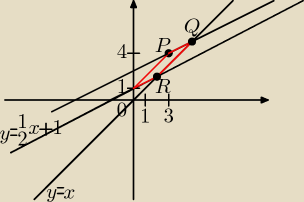Krzych: Jeden wierzchołek równoległoboku ma współrzędne P=(3,4) to wiemy z treści. Ponieważ jeden bok tego równoległoboku leży na prostej y=x a drugi na prostej y=¹₂x+1 to jeden z wierzchołków tego równoległoboku będzie leżał na przecięciu się tych prostych. Nazwijmy ten punkt R. Obliczmy zatem jego współrzędne: y=x y=¹₂x+1 −y=−x y=¹₂x+1 0=−¹₂x+1 ¹₂x=1 x=2 x=2 y=x x=2 y=2 Zatem R=(2,2) Teraz możemy napisać równanie prostej przechodzącej przez punkt P=(3,4) i równoległej do prostej y=¹₂x+1 Na niej będzie leżał kolejny bok naszego równoległoboku. y=¹₂x+b P=(3,4) 4=³₂+b b=2¹₂ y=¹₂x+2¹₂ Teraz policzymy punkt przecięcia się tej prostej z prostą y=x i otrzymamy punkt Q y=x y=¹₂x+2¹₂ −y=−x y=¹₂x+2¹₂ 0=−¹₂x+2¹₂ ¹₂x=2¹₂ x=5 x=5 y=x x=5 y=5 Zatem Q=(5,5) Teraz aby policzyć pole równoległoboku policzymy długość jednego z jego boków, czyli odcinka |QR| oraz długość wysokości poprowadzonej na ten bok czyli odległość punktu P od prostej y=x |QR|=√(5−2)²+(5−2)² |QR|=3√2

	|−1*3+1*4+0|
h=
	√(−1)2+12

	|1|
h=
	√2

	√2
h=
	2

P=|QR|*h

	√2
P=3√2*
	2

P=3

mariolka: Krzych dziękuję Ci bardzo

Marti: Nie rozumiem sposobu obliczania wysokości, czy ktoś jest na tyle miły i mógłby mi to wytłumaczyć?

Gustlik: Marti − wzór na odległość punktu od prostej: https://matematykaszkolna.pl/strona/1249.html . Poza tym można nieco prościej, bez liczenia odcinków − metodą wektorową − tutaj wyjaśnienie tej metody https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 : Punkty wyznaczamy tak, jak zrobił to Krzych: P=(3,4) − z treści zad., Q=(5,5) R=(2,2) Liczę współrzędne wektorów QP^→ i QR^→: QP^→=[3−5, 4−5]=[−2, −1] QR^→=[2−5, 2−5]=[−3, −3] Wyznacznik wektorów: d(QP^→, QR^→)= | −2 −1 | | −3 −3 | =(−2)*(−3)−(−1)*(−3)=6−3=3 Pole = |d(QP^→, QR^→)|=|3|=3