Ile punktów wspólnych ma okrąg o równaniu (x-3)^2 + (y+6)^2 = 10 z osiami współr Sławek: Ile punktów wspólnych ma okrąg o równaniu (x−3)² + (y+6)² = 10 z osiami współrzędnych? Mógłby mi ktos to obliczyć? Z góry śliczne dzięki i pozdrawiam!

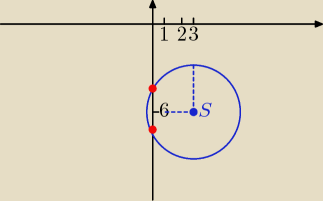
Krzysiek: środek okręgu to punkt (3,−6) promień okręgu to √10 narysuj to Sobie

toja:

Sławek: wychodzi mi, że 2 − czy to prawda?

Sławek: oo dziękuje bardzo

Aga: Możesz narysować okrąg o środku S(3,−6) i promieniu r=√10

-:): albo podstawiając x=0 ... policz punkty wspólne z osią 0y i za y=0 ... punkty wspólne z 0x

toja:

Sławek: Chociaz przyznam szczerze, ze liczyłem to troche na około. ale tez mi wyszło. najpierw podstawiłem za x 0 i wyliczyłem y i Δ była >0 więc dwa pkt. wspólne a poźniej za y podstawiłem 0 i liczyłem x i Δ była mniejsza od 0 więc 0 pkt. wspólnych więc w sumie 2 pkt. wspolne. Wiec chyba tak tez mozna, prawda ? Chociaz troche naokoło xD