ostrosłupy bas890: Pilne 1.Wyznacz objętość oraz miarę kąta miedzy ścianą boczną i płaszczyzną podstawy ostrosłupa prawidłowego sześciokątnego, wiedząc że pole jego podstawy jest równe 24√3, a pole powierzchni bocznej ostrosłupa jest równe 36. 2.W ostrosłupie prawidłowym sześciokątnym krawedź boczna ma dł.12 i jest nachylona do plaszczyzny podstawy pod kątem o mierze 60stopni.Oblicz objętość i pole powierzchni bocznej tego ostroslupa. 3.Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy pod kątem o mierze 45stopni, a wysokość tej ściany poprowadzona z wierzchołka ostrosłupa ma długość 3√2,Wyznacz, objętość i pole powierzchni całkowitej tego ostrosłupa. Bardzo prosze o pomoc jesli ktoś wie jak zrobić te zadania i niech pomoże PLISS <prosi >

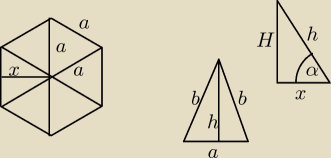Krzych: Wydaje mi się, ze w zadaniu pierwszym źle napisałeś dane, bo pole powierzchni bocznej ostrosłupa nie może być mniejsze niż pole podstawy zaś 36<24√3 Gdyby wysokość ostrosłupa prawidłowego była nieskończenie mała to pole powierzchni bocznej byłoby zbliżone do pola podstawy, ale nigdy nie byłoby mniejsze. Zaraz Ci to ładnie wykażę, słuchaj; Zauważmy, że jeżeli ostrosłup jest prawidłowy to jego podstawa jest sześciokątem foremnym o boku, który możemy oznaczyć jako a, zatem składa się z sześciu przystających trójkątów równobocznych o boku a. Pole trójkąta równobocznego o boku długości a wyraża się wzorem

	a2√3
		zatem otrzymujemy pierwsze równanie:
	4

	a2√3
6*		=24√3 Po przekształceniu tego równania otrzymujemy a=4
	4

Teraz zauważmy, że powierzchnia boczna tego ostrosłupa składa się z sześciu przystających trójkątów równoramiennych o podstawie długości a i wysokości opuszczonej na tą podstawę o długości h, zatem korzystając ze znajomości najbardziej podstawowego wzoru na pole

	1
trójkąta (P=		ah) możemy ułożyć następne równanie:
	2

	ah
6*		=36
	2

ah=12 4h=12 h=3 Teraz korzystając z wniosku z twierdzenia Pitagorasa możemy obliczyć wysokość ostrosłupa, którą oznaczyłem jako H, lecz w tym celu trzeba najpierw obliczyć długość odcinka oznaczonego przeze mnie jako x. Zauważmy, że jest to wysokość trójkąta równobocznego o boku a,

	a√3
zatem wyraża się wzorem x=		. Po przekształceniu tego wzoru otrzymujemy x=2√3
	2

H=√h²−x² H=√3²−(2√3)² H=√9−12 H=√−3 i tu właśnie pojawia się sprzeczność, o której mówiłem na początku. Tego zadania nie da się rozwiązać.

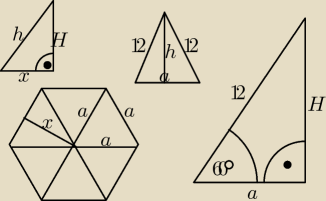Krzych: Przy rozwiązywaniu tego zadania należy pamiętać, że podstawa ostrosłupa prawidłowego sześciokątnego jest sześciokątem foremnym, zatem składa się z sześciu przystających trójkątów równobocznych, zaś powierzchnia boczna składa się z sześciu przystających trójkątów równoramiennych. Z zależności między bokami w trójkącie o kątach 30, 60, 90 stopni mamy:

	12
a=		czyli a=6
	2

oraz: H=a√3 czyli H=6√3 Teraz możemy już policzyć pole podstawy potrzebne do policzenia szukanej objętości:

	a2√3
Pp=6*
	4

	62√3
Pp=6*
	4

	36√3
Pp=6*
	4

P_p=54√3 Teraz policzenie objętości to już bułka z masłem: V=P_p*H V=54√3*6√3 V=972 Teraz policzymy pole powierzchni bocznej tego ostrosłupa. Najpierw należy znaleźć długość odcinka x. Zauważmy, że jest to wysokość trójkąta równobocznego o boku a zatem:

	a√3
x=
	2

	6√3
x=
	2

x=3√3 Teraz korzystając z twierdzenia Pitagorasa policzymy wysokość ściany bocznej, którą oznaczyłem jako h: h=√H²+x² h=√(6√3)²+(3√3)² h=√135 h=3√15 Teraz korzystając z poznanego w podstawówce wzoru na pole trójkąta liczymy pole powierzchni bocznej tego ostrosłupa:

	ah
Pb=6*
	2

P_b=3*6*3√15 P_b=54√15

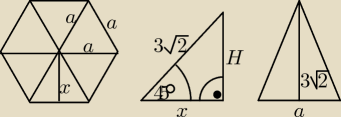Krzych: Przy rozwiązywaniu tego zadania należy pamiętać, że podstawa ostrosłupa prawidłowego sześciokątnego jest sześciokątem foremnym, zatem składa się z sześciu przystających trójkątów równobocznych, zaś powierzchnia boczna składa się z sześciu przystających trójkątów równoramiennych. Z zależności między bokami w trójkącie o kątach 90, 45, 45 stopni mamy:

	3√2
x=
	√2

x=3 Oraz: H=x H=3 Po zauważeniu, że x jest wysokością w trójkącie równobocznym o boku a możemy dzięki znajomości wzoru na wysokość trójkąta równobocznego ułożyć następujące równanie:

	a√3
x=
	2

	a√3
3=
	2

	6
a=
	√3

	6√3
a=
	3

a=2√3 Teraz korzystając ze wzoru na pole trójkąta równobocznego w prosty sposób możemy policzyć pole podstawy:

	a2√3
Pp=6*
	4

	(2√3)2*√3
Pp=6*
	4

	12√3
Pp=6*
	4

P_p=6*3√3 P_p=18√3 Teraz policzymy pole powierzchni bocznej:

	ah
Pb=6*
	2

	2√3*3√2
Pb=6*
	2

P_b=3*6√6 P_b=18√6 Teraz policzymy pole powierzchni całkowitej tego ostrosłupa: P_c=P_p+P_b P_c=18√3+18{6} P_c=18√3(1+√2) Na koniec zajmiemy się objętością: V=P_p*H V=18√3*3 V=54√3

bas890: dziękuje

Krzych: Teraz zauważyłem, że wkradł mi się mały błąd kosmetyczny. Przecież objętość ostrosłupa wyraża się wzorem V=¹₃P_p*H a nie tak jak napisałem V=P_p*h a co za tym idzie w zadaniu 2 objętość ostrosłupa wyniesie nie 972 lecz 324 zaś w zadaniu 3 nie 54√3 lecz 18√3

jakub: powinno byc V=16√3 wiec gdzies jest blad szukajcie a znajdziecie , pozdrawiam, jakub

Krzych: aach.. masz racje jakubie, popelnilem blad, przepraszam i dziekuje za poprawe