twierdzenie sinusów? FredS: Udowodnij że jeżeli. α, β są miarami kątów trójkąta, to sinα + sinβ> sin ( α+β)

Rivek: podstawiasz sin(α+β)=sinαcosβ+cosαsinβ sinα+sinβ>sinαcosβ+cosαsinβ porządkujemy i wyciągamy przed nawias sinα(1−cosβ)+sinβ(1−cosα)>0 Zauważmy, że wartość cosinusa jest maksymalnie 1. tak więc mamy dodawanie czynników większych lub równych zero. czyli jedyny problem gdy było by 0. Ale zauważmy, że cosx=0 dla 90^o, no, a dwa kąty w trójkącie nie mogą być proste. Stąd niemożliwa jest opcja, że sinα(1−cosβ)+sinβ(1−cosα)=0

Danieloo: sin(α+β)=sinαcosβ+sinβcosα Skoro α i β są miarami kątów trójkąt to cosβ i cosα są liczbami mniejszymi od 1, więc jeżeli pomnożysz sinα i sinβ przez coś mniejszego od 1 to dostaniesz coś mniejszego od sinα i sinβ.

Rivek: Oczywiście, wartość sinx dla x∊(0,π) też jest dodatnia, co należy podkreślić.

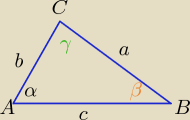
toja: a+b >c i γ= 180^o−(α+β) sin(180^o−(α+β))= sin(α+β) ze wzoru sinusów :

a		b		c
	=2R ,		=2R,		= 2R ,
sinα		sinβ		sinγ

R >0 −−− dł. promienia okręgu opisanego na tym trójkącie zatem a= 2R*sinα, b= 2R*sinβ , c= 2R*sin(α+β) z warunku trójkąta a+b>c 2R*sinα+2R*sinβ>2R*sin(α+β) /:2R sinα+sinβ> sin(α+β) c.n.u.