 zad 1/ Wykaż,że liczba √102+0,5log16 jest naturalna
zad 1/ Wykaż,że liczba √102+0,5log16 jest naturalna
 Bo już miałem iść ale topic zauważyłem
Bo już miałem iść ale topic zauważyłem 



 więc proszę nie ruszać
więc proszę nie ruszać 
 2log4sin18o = log4(sin18o)2
Zmieniam podstawę na 2: (log24 = x ⇒ x = 2 )
2log4sin18o = log4(sin18o)2
Zmieniam podstawę na 2: (log24 = x ⇒ x = 2 )
| log2(sin18o)2 | 2log2sin18o | ||
= | = log2sin18o | ||
| log24 | 2 |
| 2sin36o * cos36o * cos72o | ||
cos36o * cos72o = | = | |
| 2sin36o |
| sin72o * cos72o | 2sin72o*cos72o | |||
= | = | = | ||
| 2sin36o | 4sin36o |
| sin144o | sin36o | 1 | ||||
= | = | = | ||||
| 4sin36o | 4sin36o | 4 |
| 1 | ||
(*) = log2 | = y | |
| 4 |
| 1 | ||
2y = | ||
| 4 |
| 1 | ||
2y = | ||
| 22 |
 (Bardziej chyba się już tego rozpisać nie da
(Bardziej chyba się już tego rozpisać nie da  )
)
 Eto mogłabyś również sprawdzić te zadania co dałaś dla Kasi w innym Twoim temacie
Eto mogłabyś również sprawdzić te zadania co dałaś dla Kasi w innym Twoim temacie  Zadanie 1 (rys. wyżej)
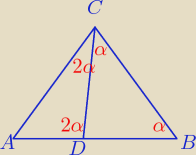
Wpierw w trójkącie BDC wiemy, że |CD| = |BD|, dlatego kąty ∡DBC i ∡BCD są równe = α.
Suma kątów w trójkącie to 180o, zatem kąt ∡BDC = 180o − 2α.
Rozpatrzymy teraz trójkąt ADC, gdzie kąt ∡ADC wynosi 2α (dlatego, że jest to kąt półpełny
Zadanie 1 (rys. wyżej)
Wpierw w trójkącie BDC wiemy, że |CD| = |BD|, dlatego kąty ∡DBC i ∡BCD są równe = α.
Suma kątów w trójkącie to 180o, zatem kąt ∡BDC = 180o − 2α.
Rozpatrzymy teraz trójkąt ADC, gdzie kąt ∡ADC wynosi 2α (dlatego, że jest to kąt półpełny  )
Skoro rozpatrujemy ten trójkąt to wiemy, z polecenia, że |AC| = |AD| dlatego kąt ∡ACD oznaczam
również 2α. Pozostało rozpatrzyć kąt ∡CAB = 180o − 4α.
Z własności trójkąta równoramiennego wiemy, że |∡A| = |∡B|, zatem:
180o − 4α = α
180o = 5α
α = 36o
|∡CAB| = 180o − 4*36o = 180o − 144o = 36o
c.n.u.
)
Skoro rozpatrujemy ten trójkąt to wiemy, z polecenia, że |AC| = |AD| dlatego kąt ∡ACD oznaczam
również 2α. Pozostało rozpatrzyć kąt ∡CAB = 180o − 4α.
Z własności trójkąta równoramiennego wiemy, że |∡A| = |∡B|, zatem:
180o − 4α = α
180o = 5α
α = 36o
|∡CAB| = 180o − 4*36o = 180o − 144o = 36o
c.n.u. 
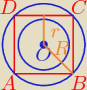 Zadanie 2
Z rysunku, można zobaczyć, że promień okręgu opisanego na kwadracie jest dokładnie połową jego
przekątnej. Natomiast promień okręgu wpisanego w kwadrat, jest dokładnie połowa boku kwadratu.
Z tych informacji otrzymuję (bok kwadratu oznaczam jako a):
Zadanie 2
Z rysunku, można zobaczyć, że promień okręgu opisanego na kwadracie jest dokładnie połową jego
przekątnej. Natomiast promień okręgu wpisanego w kwadrat, jest dokładnie połowa boku kwadratu.
Z tych informacji otrzymuję (bok kwadratu oznaczam jako a):
| a√2 | ||
R = | ||
| 2 |
| a | ||
r = | ||
| 2 |
| a√2 | a | ||
* | = √2 | ||
| 2 | 2 |
| a2√2 | |
= √2 / * 4 | |
| 4 |


 Powinno starczyć
Powinno starczyć 
| 1 | ||
sinα * sinβ = | ||
| 2 |
| 1 | ||
sinα * sin(90o − α) = | ||
| 2 |
| 1 | ||
sinα * cosα = | ||
| 2 |
| a | 1 | ||
* U{b}{c] = | |||
| c | 2 |
| a * b | 1 | ||
= | |||
| c2 | 2 |
 c.n.u.
c.n.u.  (można też nie korzystać z wzoru redukcyjnego tylko obliczyć sinβ)
To zadanie najmniej chyba było rozwinięte
(można też nie korzystać z wzoru redukcyjnego tylko obliczyć sinβ)
To zadanie najmniej chyba było rozwinięte  w tamtym temacie
Rysunek nie jest trudno narysować tylko dużo czasu zajmuje
w tamtym temacie
Rysunek nie jest trudno narysować tylko dużo czasu zajmuje



 w nagrodę
w nagrodę  pozdrawiam
pozdrawiam