stereometria Basiek: Stereometria: Ściany boczne ostrosłupa prawidłowego czworokątnego są trójkątami równobocznymi o boku dł. a. Oblicz pole przekroju tego ostrosłupa płaszczyzną nachyloną do podstawy pod kątem 45st. i zawierającą jej przekątną. Moja ogromna prośba− w jakiś cudowny sposób wyjaśnić mi jak, gdzie/ narysować tę płaszczyznę.

świąteczny ICSP: Czary mary, pokus pokus. Nie rysuję na tym złomie już więcej

Basiek: Pfff, gdzież magia tych świąt? Podziel się radością i wiedzą, czy coś Swoją drogą, wiem co to znaczy coś tu narysować. Ktoś o słabych nerwach może dostać jakiegoś wylewu, czy zawału

ZKS: Święta już się skończyły niestety.

Basiek: ZAUWAŻ, że mój post został dodany równo o północy Doszukując się pewnej analogii z "Linia należy do boiska" , mogę z całą pewnością stwierdzić, ze pisałam to w święta.

ZKS: Hmm godzina 00:00:01 już niestety należy do dnia dzisiejszego.

Basiek: Pisałam to PRZED, więc... sam rozumiesz. W ogóle ZKS z serii "mądrość ludowa": kobieta ma zawsze rację, nawet jak jej nie ma. Poza tym jest wolne= prawie jak święta Ta teoria jest naciągana, ale cóż, pewnoe mogłabym wymyślić jeszcze kilka innych. ^^

ZKS: Rozumiem więc dlatego mały prezent ode mnie: http://imageshack.us/photo/my-images/542/przekroj.jpg/. Tak mniej więcej według mnie będzie wyglądał ten przekrój. Chociaż geometria przestrzenna i zwykła nie są moimi ulubionymi rozdziałami teraz się doskonalę dzięki geometrii wykreślnej.

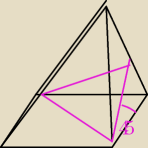
Basiek: Dobra xD Co prawda to jest średnio szczęśliwy rysunek, ale : czy o to tu chodzi?

Basiek: Ojej, jakie ładne Dziękuję, strasznie. Naprawdę. Cóż, moja stereometria to jedynie to, co zostało z gimnazjum, cała reszta dopiero za kilka miesięcy

ZKS: Ojj tam ojj tam ładne. Dziękować za . U mnie tak samo było więc wyszystko jeszcze na spokojnie opanujesz jeśli tylko będziesz chciała bo mi jakoś ten rozdział średnio się chciało opanowywać.

Basiek: Ja nie posiadam wyobraźni przestrzennej. Wydaje mi się, ze to trzeba rozwijać, ale jakoś nie bardzo miałam okazję. Cóż− sama sobie powtarzam, że mam jeszcze czas Gorzej z angielskim, tam nie umiem nic. W matmie mam takie "białe plamy" na mapie mojej wiedzy. Trygonometria, logarytmy i stereometria. No i dowodzenie jako takie

ZKS: Ja też jej nie posiadam ale teraz już jest trochę lepiej dzięki rysunkom ponieważ u mnie na studiach jest wymagana i to bardzo. Z czym jest gorzej to trzeba przysiąść i zrobić po kilka − naście zadań.

Basiek: Od 1wszej klasy nadrabiam braki z gimnazjum. Cuuudowna rzecz, naprawdę. Już wolę ślęczeć po nocach i pracować na bieżąco niż cokolwiek nadrabiać Z ciekawości, ile robisz takich zad. dziennie, żeby mieć coś zrobione "pod zajęcia"? Btw. tę stereometrię chyba sobie póki co odpuszczę. Niemal zjadłam już cały ołówek.

ZKS: Z geometrii wykreślnej musiałem robić co tydzień 1 serię zadań żeby na spokojnie je robić a że zrobiłem sobie zaległości to niestety ale w wolne będę musiał po nadrabiać zaległości czyli 6 serii muszę zrobić w tydzień żeby później mieć na razie spokój. Z rysunku jakoś tak łatwiej jest chociaż teraz facet nas zaczął poganiać i musimy zrobić w 2 tygodnie 3 rysunki.

Basiek: Systematyczność To coś, czego nigdy mieć nie będę. Cóż, zazdroszczę. Z tego, co widzę, to sporo pracy tam macie..., ale cóż ważne, że się lubi to co robi

ZKS: Początek był ciężki powiem szczerze ale im więcej tych rysunków zacząłem robić to i przyjemność dawały teraz też już wiem jak mogę coś narysować a jak nie powinienem. A systematyczności też niestety jeszcze nie posiadam ale mam nadzieje że jakoś na studiach się tego nauczę chociaż nie wiem czy nie będzie za późno niestety. Tak już jest na studiach wszędzie jest ciężko jeden przedmiot idzie łatwiej drugi natomiast wcale.

Basiek: Grunt to się dostać, potem jak się chce, to się da radę. To jest moja filozofia życiowa. Mam problem tylko z punktem a) dostać się. No cóż, jeszcze "aż" 129 dni.

ZKS: Dostać to jedno utrzymać na studiach to druga rzecz która również sprawia problemy. Zadanie dla Ciebie Wykaż że n³ + 5n jest podzielne przez 6 dla n ∊ ℕ.

Basiek: Ojeeej, ojeeej. To trudne jest tak na oko. Nie ten poziom Na poziomie maturalnym to powinno mieć postać łatwo i szybko rozkładalną do n(n+1)(n+2)

ZKS: Dam wskazówkę żebyś zastosowała metodę odejmowania i dodawania.

Basiek: Noo, toż właśnie kombinuję, co by tu dodać/ odjąć, aczkolwiek nie doszłam do niczego konstruktywnego.

ZKS: To zapisuje tutaj a Ci podpowiem.

Basiek: Hm, najrozsądniejszy wydaje mi się rozkład n³ + 9n−4n Tylko nie wiem, czy okej, dalej liczę na kartce, ale póki co, nic ładnego mi nie wychodzi

ZKS: Nie spróbuj inaczej chociaż dobrze kombinujesz że z n.

Basiek: Czy to naprawdę jest Twój ulubiony dział?

ZKS: Nie ale te zadania najbardziej pomagają w innych "poszerzają horyzonty". Później zobaczysz jak dobrze takie zadania opanujesz będzie Ci ogółem łatwiej bo będziesz znała różne sztuczki które można zastosować.

Basiek: Dobra, nie znam liczb, które mają więcej wspólnego ze wzorami skróconego mnożenia, 5−tką i 6−tką, przysięgam. n³−16n+36n−9n−6n PS. Ja nie chcę poszerzać horyzontów, chcę zdać maturę

ZKS: Rozszerzenie zawsze zdasz więc musisz poszerzyć żeby zdać dobrze maturę. Ale istnieje więcej wzorów skróconego mnożenia. Pomyśl sobie jaką liczbę należy odjąć i dodać abyś mogła z jednej zrobić liczbę podzielną przez 6 a drugą w połączeniu z n³ żeby również dała podzielną przez 6.

Basiek: Przypomniała mi się teraz piosenka "Mów do mnie jeszcze" n³−n+6n=n(n−1)(n+1)+6n (n−1)n(n+1) − podzielne 6n− podzielne suma− podzielna.

ZKS: Właśnie o to chodziło a teraz powiedz czemu (n − 1)n(n + 1) jest podzielne przez 6.

Basiek: są to 3kolejne liczby naturalne, stąd jedna z nich jest podzielna przez 2 , jedna z nich podzielna przez 3. Iloczyn tych liczb jest więcej podzielny przez 6. Co jest zabawne, 6 i 1−nkę rozpatrywałam jako przypadek drugi, zaraz po 4 i 1−nce. Tylko w moich przekształcaniach doszłam do pierwiastków i się zniechęciłam.

ZKS: Nigdy nie można się zniechęcać. Jeżeli chcesz jeszcze jakieś zadanie to napisz to za chwilkę wrzucę.

Aga: Basiek, wydaje się, że ten kąt z 00:26 jest źle zaznaczony.Kąt α to kąt dwuścienny między płaszczyzną podstawy i płaszczyzną przekroju ( między wysokością trójkąta będącego przekrojem,

	1
a		przekątnej podstawy)
	2