 Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy
pod kątek 30o, a jej wysokość jest równa 3√3. Oblicz objętość i p−całkowite
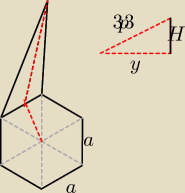
H − wysokość ostrosłupa
y − wysokość podstawy (trójkąta równobocznego)
yb − wysokość ściany bocznej (3√3)
Ściana boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do płaszczyzny podstawy
pod kątek 30o, a jej wysokość jest równa 3√3. Oblicz objętość i p−całkowite
H − wysokość ostrosłupa
y − wysokość podstawy (trójkąta równobocznego)
yb − wysokość ściany bocznej (3√3)
| H | ||
sin30o= | ||
| 3√3 |
| 3√3 | ||
H = | ||
| 2 |
| y | ||
cos30o = | ||
| 3√3 |
| a√3 | ||
4,5 = | <−−−− wzór na wysokość trójkątna równobocznego | |
| 2 |
| a2√3 | ||
Pp= | * 6 | |
| 4 |
| 27√3 | ||
Pp = | * 6 | |
| 4 |
| 162√3 | ||
Pp = | ||
| 4 |
| a | ||
Pb = 6* | * h | |
| 2 |
| 3√3 | ||
Pb = 6* | * 3√3 | |
| 2 |
| 1 | ||
V = | * Pp * H | |
| 3 |
| 81√3 | 3√3 | |||
V = | * | |||
| 3 | 2 |
| 81√3 * √3 | ||
V = | ||
| 2 |
| 243 | ||
V = | cm3 | |
| 2 |
| 81√3 | ||
Tak, Pp= | , a nie 81√3. | |
| 2 |
 dzieki za pomoc
dzieki za pomoc 