własności prawdobopodobieństwa Malwinka: Korzystając z tego, że dla dowolnych zdarzeń A,B⊂Ω mamy: A=(A\B)∪(A∩B) uzasadnij prawdziwość wzoru: P(A\B)=P(A)−P(A∩B) P(A)=(A\B)+(A∩B) P(A\B)=(A\B)+(A∩B)−P(A∩B) P(A\B)=P(A\B)

Aga: P(A)=P((A−B)∪(A∩B)) P(A)=P(A−B)+P(A∩B), bo prawdopodobieństwo sumy zdarzeń rozłącznych jest równe sumie prawdopodobieństw. Stąd P(A−B)=P(A)−P(A∩B)

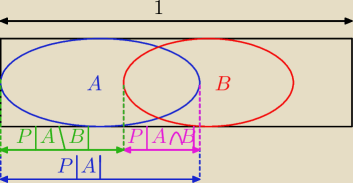
Gustlik: Można to odczytać z rysunku − cały prostokąt to Ω.