Stereometria Danieloo: Kula wpisana w stożek na pole powierzchni dwa razy mniejsze od pola powierzchni całkowitej stożka. Oblicz cosinus kąta nachylenia tworzącej tego stożka do jego podstawy. Jakiś pomysł?

Danieloo: Chociaż jakaś wskazówka, bo mi zupełnie złe wyniki wychodziły?

Krzysiek: a masz odpowiedź do tego zadania?

Krzysiek: tak na szybkiego mi wyszło: √5−2 więc trochę dziwnie...

Danieloo: Odpowiedź to ¹₃.

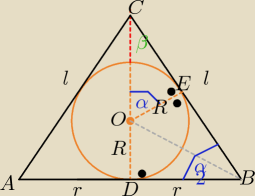
toja: Proponuję np. tak: r −−− dł. promienia podstawy stożka R −− dł. promienia kuli z warunku zadania: πr(r+l)= 2*4πR² ⇒ r²+r*l= 8R² (**) ΔOEC ~ ΔDBC |∡EOC|= |∡DBC|= α

	R		α		α
z ΔDBO		=tg		⇒ R= r*tg
	r		2		2

	r		r
z ΔDBC		= cosα ⇒ l=
	l		cosα

podstawiając do (**) otrzymujemy:

	r		α
r2+r*		= 8r2*tg2		/ : r2
	cosα		2

	1		α
1+		= 8tg2
	cosα		2

	α		1−cosα
zastępujemy: tg2		=		( wykaż sobie tę tożsamość)
	2		1+cosα

	cosα+1		8(1−cosα)
		=
	cosα		1+cosα

po przekształceniach: 9cos²α−6cosα+1=0 ⇒ (3cosα−1)²=0 ⇒ 3cosα= 1

	1
to: cosα=
	3

pozdrawiam

Danieloo: Niesamowita robota, należą się wielkie barawa, dziękuje. Problem polega na tym, że na pewno bym nie wpadł na coś takiego, a już na pewno na maturze w zadaniu ze stereometrii nie będę udowadniał tożsamości trygonometrycznej haha, chociaż może....

toja: Prosta tożsamość Często pisałam........... warto zapamiętać,że

	α		α
1+cosα=1+2cos2		−1=2cos2
	2		2

	α		α
1−cosα= 1 −(1−2sin2		)= 2sin2
	2		2

	1−cosα		α   2sin2   2		α
zatem:		=		= tg2
	1+cosα		α   2cos2   2		2

Danieloo: Nie chodziło mi o to, że tożsamość jest trudna (choć jej nie udowadniałem), tylko że nie wpadłbym na to by skorzystać z takiego pomysłu. Zakładam, że musisz być co najmniej studentką...

Godzio: Załamie Cię toja to gimnazjum

Danieloo: Niemożliwe.

Godzio:

toja:

Danieloo: W sumie to ja bym tą tożsamość ugryzł od drugiej strony, z tablic biorę tg^α₂ i dalej to już łatwizna. Ale większy problem sprawiło by mi wpadnięcie na pomysł, że 1+cosα=1+2cos^2α₂−1. Bo udowodnienie tego też nie jest trudne. Chyba trzeba mieć wyobraźnię gimnazjalisty by wpaść na coś takiego.