planimetria
Pepsi2092:
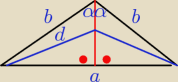
W rozwartokątnym trójkącie równoramiennym ABC ( |AC|=|BC| ) odległość środka koła wpisanego w
trójkąt wierzchołka A jest równa d, a |∡ACB|=2α. Oblicz pole trójkąta ABC i promień koła
opisanego na trójkącie ABC.
i mam pytanie takie czy jak będę chciał wyznaczyć b za pomocą a z twierdzenia cosinusów to
będzie tak :
a
2=b
2+b
2−2b
2*cos2α
czy a
2=b
2+b
2−2b
2*
− cos2α.
Niby kąt jest rozwarty to wypadałoby z tego drugiego pojechać bo cos w II ćwiartce jest ujemny.
ale niech ktoś mnie jeszcze tutaj raz upewni bo nie chce sie bez sensu naliczyć
