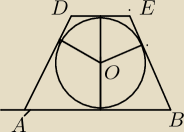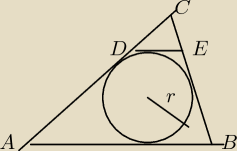
Okrąg wpisany w trójkąt hwdtel: Równoległa do podstawy AB ΔABC,w który wpisano okrąg o promieniu R i styczna do tego okręgu ,odcina z trójkąta ABC,trójkąt DEC.Wykazać,że pole ΔDEC jest równe P=¹₂(|DC|+|CE|−|DE|)r

hwdtel: r=R−oczywiście(chochlik)

x3:

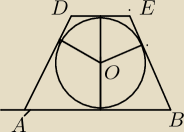
	|AB|+|AC|+|BC|
PΔABC=		r ; PΔDEC=PΔABC − PABED
	2

P_ABED =(|DE|−x)r + [|CA|−|CD|−(|DE|−x)]r + xr +[|CB|−|CE|−x]r ale ¹₂[|CA|−|CD|−x] +¹₂[|CB−|CE|−x] =AB zatem P_ABED=¹₂r[|DE|+|CA|−|DC|+|CB|−|CE|+|AB|] czyli P_ΔDEC=[¹₂|DC|+|CE|−|DE|]r cnw