... Ruda: O zdarzeniach A⊂Ω i B⊂Ω wiemy, że P(A)= ¹³₂₄, P(B\A)= ¹₃, P((A∩B)')=³₄. Oblicz P(A∪B), P(A\B), P(B') P(A∪B) = P(A) + P(B\A) P(A∪B) = ¹³₂₄ + ¹₃ = ²¹₂₄ Dalej jestem w martwym punkcie

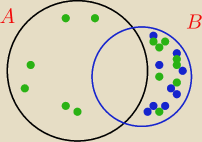
sushi_ gg6397228: kolor niebieski P(B\A) kolor zielony P(AnB')

sushi_ gg6397228: kolor zielony tylko w A= kolor zielony caly MINUS kolor niebieski policz czesc wspolna=== zbior A MINUS kolor zielony w A

Ruda: P((A∩B)') ten prim jest za nawiasem. Zaryzykowałam i... P((A∩B)') = 1 − P(A∩B) ³₄ = 1 − P(A∩B) P(A∩B) = ¹₄ P(A∪B) = P(A) + P(B) − P(A∩B) ²¹₂₄ = ¹³₂₄ + P(B) − ¹₄ P(B) = ¹⁴₂₄ P(B') = 1 − P(B) = ¹⁰₂₄ Nie wiem czy dobrze?

Ruda: P((A∩B)') = 1 − P(A∩B) nie wiem czy ten wzór jest poprawny

Basia: 1. P(A∪B) ≠ P(A)+P(B) poszukaj prawidłowego wzoru 2. P[(A∩B)'] = 1 − P(A∩B) z tego wylicz P(A∩B) 3. (B\A)∩(A∩B)=∅ i wtedy (i tylko wtedy) P[(B\A)∪(A∩B)] = P(B\A)+P(A∩B) = .... podstaw i wylicz natomiast (B\A)∪(A∩B) = B czyli P(B) = P[(B\A)∪(A∩B)] no i masz P(B) dopiero teraz możesz policzyć P(A∪B) 4. P(B') = 1−P(B) 5. A = (A\B)∪(A∩B) i są to zbiory rozłączne czyli P(A) = P[(A\B)∪(A∩B)] = P(A\B) + P(A∩B) z tego wyliczysz P(A\B)

sushi_ gg6397228: jest tak samo poprawny jak P(D')= 1− P(D) jakbys zobaczyla na kolory, to bys wiedziala, ze nawias zostal zjedzony przeze mnie P((AnB)')

Ruda: Sushi właśnie nie ogarniam Twojego rysunku

sushi_ gg6397228: masz kropki −−> niebieski i zielone

Gustlik:

	13		1		3
O zdarzeniach A⊂Ω i B⊂Ω wiemy, że P(A)=		, P(B\A)=		, P((A∩B)')=		.
	24		3		4

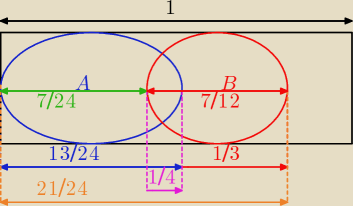
Oblicz P(A∪B), P(A\B), P(B') Najlepiej metodą "graficzna". Tę "graficzną" metodę wyznaczania prawdopodobieństwa omówiłem tutaj: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1018 Ten prostokąt to Ω. Trzeba zrobić rysunek, bo z rysunku to fajnie wyjdzie. Najpierw zanim zrobię rysunek − liczę P(A∩B), żeby wiedzieć, czy będzie część wspólna (czyli zbiory będą "nachodzić" na siebie, czy będą "leżały" obok siebie)

	3		1
P((A∩B)')=		⇒ P(A∩B)=		≠0, czyli jest część wspólna, zbiory "nachodzą" na
	4		4

siebie Liczę sumę, żeby wiedzieć, czy zbiory A i B wypełnią całe Ω, czy będzie "luka": P(A∪B) = P(A) + P(B\A)

	13		1		21
P(A∪B) =		+		=		<1, będzie więc "luka"
	24		3		24

Teraz widać, że rozmieszczenie zbiorów będzie takie, jak na rysunku. Resztę liczę geometrycznie z rysunku:

	13		1		13		6		7
P(A\B)=		−		=		−		=
	24		4		24		24		24

	1		1		4		3		7		7		5
P(B)=		+		=		+		=		⇒P(B')=1−		=
	3		4		12		12		12		12		12

	21		7		7		5
Odp: P{AUB}=		=		, P(A\B)=		, P(B')=
	24		8		24		12