najdź długość krawędzi podstawy tego ostrosłupa, który ma największą objętość. Magda: Rozważamy ostrosłupy, które w podstawie mają sześciokąt foremny, jedna z krawędzi bocznych jest prostopadła do płaszczyzny podstawy, a suma długości najkrótszej i najdłuższej krawędzi bocznej jest równa 24cm. Znajdź długość krawędzi podstawy tego ostrosłupa, który ma największą objętość.

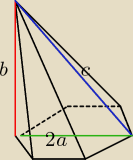
Basia: najkrótsza jest b (ta prostopadła); najdłuższa c (przeciwległa do b) b+c = 24 b² + 4a² = c² b²+4a² = (24−b)² b² + 4a² = 24² − 48b+b² 48b = 24² − 4a²

	24*24		4a2
b =		−
	48		48

poskracaj to

	1		a2√3
V =		*6*		*b
	3		4

podstaw za b i znajdź maksimum funkcji V(a)