rozwiązać równanie michu: Ix+3I=1−Ix−3I przedziały to (−∞,−3) , <−3,3) , (3,+∞) no i dla 1 wychodzi mi x= −1/2 dla 2 0= −5 − co jest sprzeczne dla 3 x =1/2 to jest ok ? czy coś jest nie tak

Basiek: Mhm, powiedz mi, dlaczego w tym, co napisałeś, 3 nie należy do żadnego przedziału? Nie liczyłam tego, od razu mówię... ale tak, jak już wyliczyłeś x, to sprawdź, czy należą do przedziału, dla którego je obliczałeś, jeśli nie, to liczby nie spełniają równania.

	1
Z tego, co zapisałeś wynika, że x=		i to jedyna odp.
	2

ICSP: równanie sprzeczne.

michu: to w tym 3 powinno być <3,+∞)

michu: ale jak to wyjaśnić że sprzeczne

ICSP: To nic nie zmienia. Sprzeczne.

Basiek: ech, fakt,zagapiłam się, 1/2 nie jest większa od 3 Dzięki, ICSP Całość faktycznie jest sprzeczna .

ICSP:

	1
x = −		∉ (−∞;3)
	2

	1
x =		∉ (3;+∞)
	2

sprzeczne. Jak już rozpatrujesz w przedziałach to rozpatrz to do końca

Basiek: @Michu− sprzeczne, bo NIE MA ROZWIĄZAŃ pierwszy pierwiastek nie należy do pierwszego przedziału −> Odpada drugi w ogóle jest sprzeczny trzeci−> patrz pierwszy x∊∅ , brak rozwiązań, nie istnieje taka liczba, równanie jest sprzeczne, ok?

michu: aha o to chodzi

michu: dzięki

Basiek: Na początku często się zapomina, że WSZYSTKO i WSZĘDZIE trzeba sprawdzać z dziedziną

michu: a te przedziały są ok (−∞,−3) , <−3,3) , (3,+∞)

Basiek: Nie, popatrz uważnie. <−3, 3) (3,+∞) Czy możesz mi powiedzieć, do którego przedziału należy u Ciebie trójka?

michu: do żadnego

Basiek: właśnie. Tak napisałeś, a przecież 3 należy do dziedziny MUSI być uwzględniona w którymś z przedziałów. Nie jest istotne, gdzie to domkniesz, ważne, że musisz domknąć w jednym LUB w drugim. Łapiesz?

michu: czyli gdzieś trzeba ta 3 mieć i to obojętne czy w 2 czy w 3 − tych przedziałów to nie bardzo rozumiem

michu: teraz tak−−−−−− bo pierwsze ustalam a pózniej liczę

Basiek: Tak, dokładnie Twoją dziedziną dla całości był przedział (−∞.+∞), a 3 z pewnością do niego należy. Więc przypoprawianiu: może być tak: <−3, 3> (3,+∞) lub tak <−3, 3) <3,+∞) Zrobisz więcej przykładów, to sobie to wszystko ułożysz w głowie, spokojnie

michu: aha no teraz wiem co z czym

Basiek: To dobrze, powodzenia dalej

michu: a takie coś f(x)=I2/x−1I − 2 funkcje wiem jak zrobić tylko chodzi o takie coś . napisz wzór funkcji y=g(m) opisującego liczbę rozwiązań równania f(x)=m w zależności od parametru m , no i zrobić wykres mam przykłady ale dla mnie to czarna magia − nie jestem w stanie odczytać ten wykres

wik_gg8947201: najpierw ustal, dla jakich x wyrazenie 2/x−1≥0

Basiek: Już piszę. Całość polega w zasadzie na narysowaniu wykresu. zaczynasz od samego od ZAŁOŻEŃ (zawsze i wszędzie x≠1 (wynika z mianownika) teraz "rozkładasz" sobie Twoją funkcję na czynniki

	2
zacznij od narysowania		−> homograficzna, asymptota pionowa w 1, podstaw sobie kilka
	x−1

punktów i rysuj Jak bd mieć, napiszę , co dalej

michu: chwila 2/x − 1 czyli o 1 w dół

wik_gg8947201: Mozna narysowac ta funkcje homograiczna, nastepnie ujemne wartosci zaznaczyc symetrycznie wzgl osi OX i caly wykres przesunac o 2 w dol

Basiek: czekaj, czekaj.

	2
to jest a)		, czy
	x−1

	2
b)		−1
	x

?

wik_gg8947201: a to pionowa x=0 czyli OY oraz pozioma y=−1, bo w mianowniku jest tylko x?

michu: wykres wiem jak zrobić ale to y= g(m) − jak za to się zabrać

michu: b

michu: mój błąd − sory

wik_gg8947201: potem patrzysz w ilu punktach bedzie przecinala ten wykres prosta pozioma y=m

michu: x≠0 − założenie

wik_gg8947201: tak

michu: prosta pozioma y=m − co to jest ?

wik_gg8947201: w zaleznosci od wartosci np. y=−3 w ilu p bedzie przecinala otrzymany wykres, to tyle bedzie rozwiazan

michu: no właśnie w zależności od wartości a gdzie ta wartość jest lub gdzie powstaje na wykresie czy gdzie ?

wik_gg8947201: zobaczysz jak zrobisz wykres poprawnie, dla m<−2 brak rozw. dla m=−2 jedno rozw. itd.

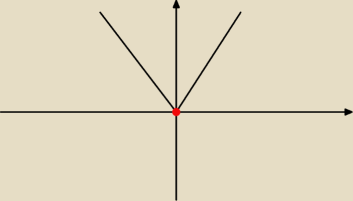
Basiek: Ja to rozumiem trochę inaczej... cięzko to trochę wytłumaczyć, ale może akurat Patrzysz na oś Y , przy jakich y−kach masz jakąś część wykresu? np tu. Wykresu w ogóle nie ma poniżej osi X... czyli (to już dla wykresu g(m)) 0 rozw. dla x∊(−∞,0) 1 rozw. dla x=0 2 roz. dla x∊(0,+∞) I właśnie to zaznaczasz na drugim wykresie...

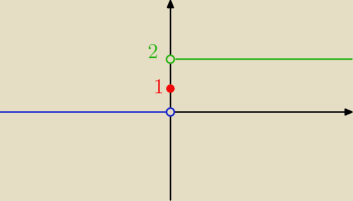
Basiek: Dla tego powyżej wykres g(m) będzie wyglądać tak:

michu: 2 roz. dla x∊(0,+∞) − gdzie to to chodzi o przecięcie z tą y=m 0 rozw. dla x∊(−∞,0) − bo nigdzie nie przecina 1 rozw. dla x=0 punkt (0,0) 2 roz. dla x∊(0,+∞) a to i czy dobrze to rozumiem

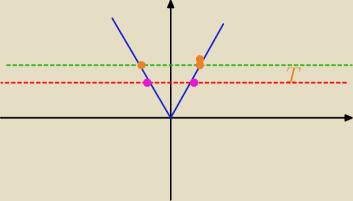
Basiek: te proste przerywane, to te proste z parametru m. Chyba o to chodziło z przecinaniem się.... Wiesz co? Trochę zamieszałam, pomyliłam się, chodzi o to, że 0 rozw. dla x∊(−∞,0) − bo nigdzie nie przecina 1 rozw. dla x=0 punkt (0,0) 2 roz. dla x∊(0,+∞) a to Wszędzie , gdzie jest x−> należy zamienić literkę na m , bo nasz wykres to g(m), m jest naszą zmienną. Pewnie ten x w zapisie jakoś przy przeszedł, ale w całości mając zadanie− powinno być m! Przepraszam,

Basiek: A to T−> musiałam kliknąć przez przypadek przy wysyłaniu.

michu: te proste przerywane, to te proste z parametru m. jak to m wyliczyć wyznaczyć −bo teraz to nic nie wiem

Basiek: Właśnie dlatego nie znalazłam tłumaczenia tego w sieci. Po prostu to jest masakryczne wytłumaczyć to coś. To m to są przedziały y z pierwszego wykresu, przyjrzyj się... np. y dla (0,+∞) ma 2 rozwiązania.... co też zapisaliśmy przy m... Wybacz, naprawdę chyba nie umiem tego wytłumaczyć .

Basiek: A te proste przerywane, to były dwie dowolne proste w przedziale (0,+∞), żeby Ci pokazać, że każda z nich ma po 2 rozwiązania.

michu: nie no i tak dziękuje za próbę bo to się najbardziej liczy no i za czas który poświęciłaś dla mnie

Basiek: Nie ma za co, szkoda, ze tak wyszło. Może następnym razem wyjdzie lepiej? Całą geometrię analityczną, wykresy itd. cięzko wytłumaczyć w internecie, bo pytania w głowie tworzą się na bieżąco, a potem jakby odkładają na mały stosik... Cóż, powodzenia. Pomyśl nad tym jeszcze− po nitce do kłębka

michu: napewno się nie poddam hehe

Basiek: Aaa, jeszcze Ci napiszę, jak (chyba ) powinno wyjść Twoje zadanie

	⎧	0 dla m∊(−∞,−2>
g(m)=	⎩	2 dla m∊(−2,+∞)