funkcja wymierna
kaśka: zad1.
Sporządź wykres funkcji i opisz jej własności:
zad2.
określ zbiór liczb, dla których wyrażenie ma sens liczbowy i wykonaj działania.
| 2x3−2 | | x2+x+1 | |
| : |
| = |
| x2−5x−14 | | x2−14x+49 | |
20 gru 16:39
kaśka: 2 zestaw:
zad1.
| | 2|x|−3 | |
dana jest funkcja: f(x)= |
|
|
| | 3|x|−2 | |
a) naszkicuj wykres funkcji
b) opisz własności
c) podaj ilość rozwiązań w zależności o parametru m.
| | 2|x|−3 | |
sporządź funkcję f(m) i narysuj jej wykres: f(m)= |
|
|
| | 3|x|−2 | |
zad2.
dla jakich wartości parametru a zbiorem rozwiązań nierówności jest zbiór wszystkich liczb
| | x2+ax | |
rzeczywistych : −1< |
| <2
|
| | x2−x+2 | |
zad3.
dla jakich m istnieją 2 różne pierwiastki równania takie, że suma odwrotności tych rozwiązań
jest liczbą dodatnią?
x
2+2(m−1)x+m
2+m−2=0
20 gru 16:47
kaśka: prosiłabym o pomoc

krok po kroku

20 gru 16:47
kaśka: będzie może ktoś tak miły i pomoże

?
20 gru 18:12
ZKS:
Czego nie rozumiesz?
20 gru 18:26
kaśka: tak na prawdę to wszystkiego. chora byłam, co spowodowało nieobecność na lekcjach. i potrzebuję
aby ktoś rozwiązał mi te przykłady, a ja będę już sobie próbować inne w podobny sposób

20 gru 18:56
ZKS:
Chora nie chora trzeba to niestety umieć więc na początku rozpisz |x
2 − 1|.

20 gru 18:57
kaśka: a muszę sprawdzian zaliczyć

co nie powoduje u mnie uśmiechu

i to przed świętami

20 gru 18:58
ZKS:
Dobrze że powiedziałaś jak masz mieć sprawdzian jeszcze to powinnaś sama to rozwiązywać ja mogę
Ci pomóc.

20 gru 19:00
imralav: Co do pierwszego zadanka − założenie, że mianownik nie jest zerem, potem rozpatrujesz dwa
przypadki, gdy x2 − 1 > 0 i x2 − 1 < 0
20 gru 19:05
kaśka: aa

x
2 − 1 dla x
2 większe bądź równe 1 (czyli to zachodzi zawsze)
−(x
2 − 1) dla x
2 < 1 −−−− fałsz
20 gru 19:06
kaśka: a nie, ten drugi to poprostu x2<1
20 gru 19:07
imralav: z tym że x2 nie może być równe 1, bo wtedy w mianowniku jest zero
20 gru 19:10
kaśka: czyli jak to wychodzi?
20 gru 19:15
ZKS:
| | 1 | |
x2 − 1 > 0 nie zachodzi przecież zawsze wstaw sobie np: x = |
| i zobacz czy będzie |
| | 2 | |
większe od 0.
20 gru 19:15
ZKS:
Rozwiąż nierówność kwadratową x2 − 1 > 0 oraz x2 − 1 < 0.
20 gru 19:16
kaśka: ja zrobiła bym to tak:
|x2−1|≠0
czyli x ∊R\{1,−1}
(x−1)(x+1)=x2−1
|x2−1|=
x2−1 x∊(∞,−1) i (1,∞)
−(x2−1) x∊(−1,1)
20 gru 19:26
kaśka: pierwszy przykład:
20 gru 19:28
kaśka: potem 2:
| | x4−1 | |
y= |
| =...=−x2−1 |
| | −(x2−1) | |
20 gru 19:28
kaśka:
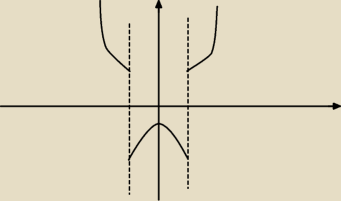
20 gru 19:33
kaśka: coś w tym stylu mi wyszło
20 gru 19:33
ZKS:

.
20 gru 19:36
kaśka: jupi

a teraz mi powiedzcie jak się dzieli te wyrażenia;>
20 gru 19:38
kaśka: a jak zrobić zad1 w 2 zestawie?
20 gru 20:16
 krok po kroku
krok po kroku 
 ?
?


 co nie powoduje u mnie uśmiechu
co nie powoduje u mnie uśmiechu i to przed świętami
i to przed świętami 

 x2 − 1 dla x2 większe bądź równe 1 (czyli to zachodzi zawsze)
−(x2 − 1) dla x2 < 1 −−−− fałsz
x2 − 1 dla x2 większe bądź równe 1 (czyli to zachodzi zawsze)
−(x2 − 1) dla x2 < 1 −−−− fałsz

 .
.
 a teraz mi powiedzcie jak się dzieli te wyrażenia;>
a teraz mi powiedzcie jak się dzieli te wyrażenia;>