nierówność, dzielenie i parametry wielomianu
Jola: Witam mam 3 zadanka które nie wiem jak obliczyć...
1) x4 − 4x3 − 5x2 + 36x − 36 >0 można korzystać ze schematu Hornera aby obliczyć
nierówność? Jeśli nie to proszę o jakąś metodę żebym mogła rozwiązać pozostałe przykłady tego
typu
2)dla jakich wartości parametrów a i b liczba 3 jest dwukrotnym pierwiastkiem wielomianu
W(x)=x3 − 5x2 + ax + b
3)wykonaj dzielenie wielomianu w(x) przez P(x) gdzie
w(x)= 5x3+ 2x2 −3x +7
p(x)= x2−4 tutaj gdy ten drugi wielomian rozłącze na x−2 i x+2 to wychodzą mi
reszty i nie wiem co dalej.... Bardzo proszę o pomoc
20 gru 09:32
wik_gg8947201: w 3) zawsze wyjdzie reszta, bo −2 lub 2 nie sa pierwiastkami wielomianu − nic dalej
20 gru 09:50
wik_gg8947201: 2) x2(x−5)+ ax+b→ax+b=6(x−5)+39 i 27−45+3a+b=0
20 gru 09:55
wik_gg8947201: 1) x1=2, szukaj dalej mz. rozlozyc na iloczyn, zbadac znaki w przedzialach i odp.
20 gru 09:59
Jola: yhym.... dziękuję bardzo za pomoc

20 gru 10:02
wik_gg8947201: w 2) (x−3)2(x−5)= ...wymnozyc i odczytac a, b
20 gru 10:03
wik_gg8947201: w 2) jednak nie bedzie tak
20 gru 10:11
Jola: hmm... a możesz mi to rozpisać tak krok po kroku jak to robisz żeby to zrozumieć?
20 gru 10:27
wik_gg8947201: w ktorym?
20 gru 10:29
Jola: 2 i 1 jeśli mogę prosić

20 gru 10:30
wik_gg8947201: w 1) podziel wielomian przez (x−2) i szukaj dalej miejsc zerowych
20 gru 10:32
wik_gg8947201: w 2) (x−3)2(x+1)=
20 gru 10:34
wik_gg8947201: a=−6
b=9
20 gru 10:37
Jola: hmm przeliczyłam to ostatnie i mi wyszło że a=−3 a b=9

20 gru 11:29
wik_gg8947201: a=3
20 gru 11:36
wik_gg8947201: bedzie −6x+9x= 3x
20 gru 11:37
wik_gg8947201: a pierwszym jakie mz wyliczylas?
20 gru 11:38
Jola: no właśnie nie wyliczyłam bo wyszła mi reszta w dzieleniu i nie wiem co trzeba zrobić z tą
resztą...

20 gru 12:03
wik_gg8947201: przeciez musi dzielic sie bez reszty, bo W(2)=0
20 gru 12:09
Jola: aaaa już wiem popełniłam błąd w liczeniu xD
20 gru 12:14
Jola: ale i tak mi wychodzi nadal reszta nie wiem gdzie popełniam błąd..

20 gru 12:16
wik_gg8947201: W(x)=(x−2)(x3−2x2−9x+18)= (x−2)2(x2−9)=...
teraz dasz rade?
20 gru 12:22
Jola: aha i mam takie jedno pytanie bo mam jeden przykład równania z wartoscia bezwzględną
| | ⎧ | |x|=a | |
| x3 − 2x2 +|3x − 6|=0 i korzystając z własności | ⎨ | | x=−a v x=a to jak powinien
|
| | ⎩ | a>0 | |
wyglądać poprawny zapis
−3x+6=−x
3 + 2x
2 czy 3x + 6= −x
3 + 2x
2 ?
20 gru 12:24
wik_gg8947201: 3x−6 dla x≥2
6−3x dla x<2
20 gru 12:25
Gustlik:
ad 1 1) x
4 − 4x
3 − 5x
2 + 36x − 36 >0 oczywiście że możesz z Hornera.
Kandydaci na pierwiastek: +−1, +−2, +−3, +−4, +−6, +−9, +−12, +−18, +−36
1 −4 −5 36 −36
1 1 −3 −8 28 −8
−1 1 −5 0 36 −72
2 1 −2 −9 18 0
x=2 jest pierwiastkiem
(x−2)(x
3−2x
2−9x+18)>0
(x−2)[x
2(x−2)−9(x−2)]>0
(x−2)(x−2)(x
2−9)>0
(x−2)
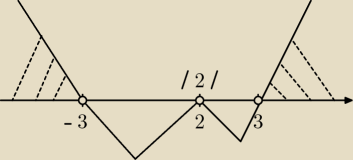
2(x−3)(x+3)>0
x=2 (2−krotny) v x=3 v x=−3
Odp{ x∊(−
∞; −3)U(3, +
∞)
21 gru 00:02





 ad 1 1) x4 − 4x3 − 5x2 + 36x − 36 >0 oczywiście że możesz z Hornera.
Kandydaci na pierwiastek: +−1, +−2, +−3, +−4, +−6, +−9, +−12, +−18, +−36
1 −4 −5 36 −36
1 1 −3 −8 28 −8
−1 1 −5 0 36 −72
2 1 −2 −9 18 0
x=2 jest pierwiastkiem
(x−2)(x3−2x2−9x+18)>0
(x−2)[x2(x−2)−9(x−2)]>0
(x−2)(x−2)(x2−9)>0
(x−2)2(x−3)(x+3)>0
x=2 (2−krotny) v x=3 v x=−3
Odp{ x∊(−∞; −3)U(3, +∞)
ad 1 1) x4 − 4x3 − 5x2 + 36x − 36 >0 oczywiście że możesz z Hornera.
Kandydaci na pierwiastek: +−1, +−2, +−3, +−4, +−6, +−9, +−12, +−18, +−36
1 −4 −5 36 −36
1 1 −3 −8 28 −8
−1 1 −5 0 36 −72
2 1 −2 −9 18 0
x=2 jest pierwiastkiem
(x−2)(x3−2x2−9x+18)>0
(x−2)[x2(x−2)−9(x−2)]>0
(x−2)(x−2)(x2−9)>0
(x−2)2(x−3)(x+3)>0
x=2 (2−krotny) v x=3 v x=−3
Odp{ x∊(−∞; −3)U(3, +∞)