planimetria
Kinga: Proszę o pomoc
Podstawą ostrosłupa jest kwadrat, a spodek wysokości znajduje się w jednym z
wierzchołków tego kwadratu. Wiedząc, że wysokość tego ostrosłupa jest równa krawędzi podstawy
oblicz:
a) miarę kąta nachylenia ścian bocznych, które nie zawierają wysokości ostrosłupa, do
płaszczyzny podstawy
b) cosinus kąta nachylenia najdłuższej krawędzi bocznej ostrosłupa do krawędzi podstawy.
19 gru 17:25
Kinga: Pomoże ktoś ?
19 gru 18:16
dero2005:
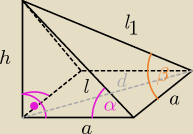
a = h
α = 45
o
d = a
√2
l
1 =
√h2 + d2 =
√a2 + 2a2 =
√3a2 = a
√3
| | a | | a | | √3 | |
cos β = |
| = |
| = |
| |
| | l1 | | a√3 | | 3 | |
19 gru 18:53
Kinga: dziękuję ogromnie
19 gru 21:28
Korek: dlaczego za kąt α obrano akurat ten skoro jest mowa o kącie nachylenia ścian bocznych ?
12 paź 16:48
Kacper:
Bo to jest ten kąt, o który proszą.
12 paź 16:58
Qulka: bo ściana boczna jest trójkątem prostokątnym i jej wysokość jest jednocześnie krawędzią
20 lut 13:12
KaroX: l1 = √h2 + d2 = √a2 + 2a2 = √3a2 = a√3
Skad pochodzi ten wzor ?
18 lis 19:14