geometria analityczna - równania okręgów stycznych do okręgu
Arynka: Mając dane współrzędne punktów A=(−3,2) i B=(1,−8) wyznacz: równania okręgów o środku w punkcie
A, stycznych do okręgu o równaniu: (x+1)2 + (y−2)2 = 9.
Wcześniej były inne podpunkty, takie jak, współrzędne środka, długość odcinka, równanie
prostej, symetralna odcinka, równanie okręgu, którego średnicą jest odcinek AB i równanie
okręgu stycznego do OY o środku w punkcie A − to zrobiłam. Na ostatnim podpunkcie poległam.
Proszę o pomoc....
19 gru 09:07
krystek: Aby okrąg był styczny do danego to odległość środków musi się równać sumie promieni LUB
różnicy promieni .
19 gru 09:10
Arynka: nadal nie rozumiem... Proszę o więcej wskazówek, albo przykład. Nie robiliśmy takiego zadania
na lekcji, w podręczniku też nie ma podobnego zadania, na stronce też.
19 gru 09:15
krystek: S=(−1;2) a srodek szukanego s2=(−3;2)
i teraz IS;S2I=r−1+r2
A można tak :
prosta przez środki S(−1,2) oraz S2(−3;2) napisać jej równanie
znaleźć punkt wspólny z danym okręgiem i odległośc tego punktu do A da Tobie długość promienia
drugiego okręgu i już z górki!
Aby łatwiej zrozumieć zrób rysunek
A ten punkt B nie gra żadnej roli bo nic o nim nie piszesz.
19 gru 09:38
krystek: Zapis wcześniej miałbyć:IS,S2I=r1+r2I
19 gru 09:39
krystek:
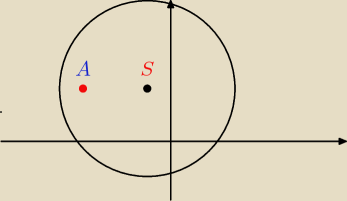
_
19 gru 09:49
krystek: I jak widać odległośc środków musi się równać RÓżnicy promieni
19 gru 09:50
Arynka: wychodzi mi prosta y=2, bo inaczej nie może być, skoro dla różnych x, wychodzi taki sam y równy
2

Policzyłam odległość między środkami A i S, wyszło mi 2
√5, a z tego IS
1; S
2I wyszło
3−2
√5
Zrobiłam rysunek, nic z niego nie wynika...

Nadal nie rozumiem, z czego mam wziąć równanie okręgów stycznych...
19 gru 10:15
krystek: I teraz wyznaczasz x punktów przecięcia :
(x+1)2+(y−2)2=9
(x+1)2+(2−2)2=9
X2+2x−8=0 Δ=36 x1=−4 x2=2
stąd punkty przecięcia to D=(−4,20 i E=(2;2)
i r2 to IDAI bo styczne tylko wewnętrznie poniewaz A leży wewnątrz okręgu.
19 gru 11:14
krystek: D=(−4;2)
19 gru 11:15
krystek: lub r2=IAEI
19 gru 15:00
 _
_
 Policzyłam odległość między środkami A i S, wyszło mi 2√5, a z tego IS1; S2I wyszło
3−2√5
Zrobiłam rysunek, nic z niego nie wynika...
Policzyłam odległość między środkami A i S, wyszło mi 2√5, a z tego IS1; S2I wyszło
3−2√5
Zrobiłam rysunek, nic z niego nie wynika... Nadal nie rozumiem, z czego mam wziąć równanie okręgów stycznych...
Nadal nie rozumiem, z czego mam wziąć równanie okręgów stycznych...