dowodzenie Aleks: Hej mam 3 zadanka i nie wiem jak się za nie zabrać... 1.wykaż,że jeżeli dla dowolnych liczb rzeczywistych x i y prawdziwa jest równośc (x−y)² +4xy=4(x+y),to .y=−x lub y=4−x, 2.wykaż,że jeśli x,y są dowolnymi liczbami rzeczywistymi oraż (x² +y²)(x+y)=2x²+2xy²,to x=y lub x=−y 3.w trapezie prostokątnym abcd kąty abc i bcd są proste,zaś podstawa ab jest dłuższa od podstawy cd.Wykaż,że AC²=BD²=AB²=DC² Z góry dzięki za pomoc!

ICSP: (x−y)² +4xy = 4(x+y) x² − 2xy + y² 4xy = 4(x+y) x² +2xy + y² = 4(x+y) (x+y)² = 4(x+y) (x+y)(x+y−4) = 0 ⇔ y = −x v y =4−x c.n.u.

ICSP: Drugie na pewno dobrze przepisane?

ICSP: Trzecie to na pewno źle przepisane.

KoreX: W Twoim drugim wierszu rozwiązania zgubiłeś + przed 4xy

Godzio:

Aleks: dzięki za pierwsze ,w drugim jest błąd powinno być (x² +y²)(x+y)=2x²y+2xy² a w trzecim dobrze przepisalem

ICSP: (x² + y²)(x+y) = 2x²y + 2xy² (x² + y²)(x+y) = 2xy(x +y) (x² −2xy + y²)(x+y) = 0 (x−y)²(x+y) = 0 ⇔ y = x v y = −x

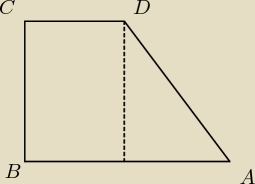
ICSP: chcesz mi powiedzieć że |AC|² = |BD|²

Aleks: tak mam napisane na kartce

Aleks: i tez się zdziwiłem

ICSP: to widocznie źle przepisałeś KoreX fakt zgubiłem ten plusik

KoreX: jak to mówią, diabeł tkwi w szczegółach

Aleks: zadanie dobrze przepisałem

Aleks: trzy razy sprawdzałem

MaciejPoznań: 2(x−y)(x+y)−3(x+2y)²+(x−y)² Mam problem z rozwiązaniem, więc gdyby ktoś pomógł to wielkie dzięki