Jak obliczyć punkt przegięcia, wklęsłości i wypukłości tej f-cji? piotrek: Jak obliczyć punkt przegięcia, wklęsłości i wypukłości tej f−cji? y= x⁴−3x²+x−1 proszę o pomoc

ZKS: Policz pochodne i punkty stacjonarne.

Gustlik: Przypomina to badanie ekstremów i monotoniczności funkcji, tylko do tego celu służy druga pochodna: y'=4x³−6x+1 y''=12x²−6 Warunek konieczny istnienia punktu przegięcia y''=0 12x²−6=0

	√2		√2
x2=		v x2=−		to są punkty "podejrzane" o punkt przegięcia
	2		2

	√2		√2
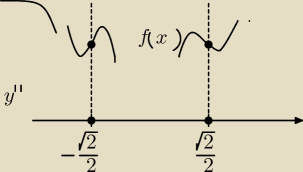
Wykres wypukły ("uśmiechnięty") gdy y''>0 dla x∊(−∞, −		)U(		, +∞)
	2		2

	√2		√2
Wykres wklęsły ("smutny") gdy y''<0 dla x∊(−		;		)
	2		2

	√2		√2
Punkty przegięcia − x2=		v x2=−		, bo wykres zmienia charakter wypukłości w
	2		2

tych punktach.

Gustlik:

	√2		√2
Mały chochlik: ma być oczywiście x=−		v x=		, a nie x2. Pozdrawiam.
	2		2

piotrek: dzięki

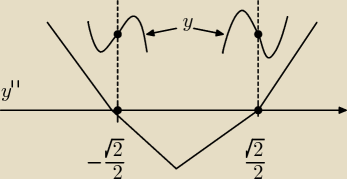Gustlik: Poprawiam rysunek, bo nie wiem, czemu mi wycięło parabolę.