dowody geometryczne
BLAZEJ_505:
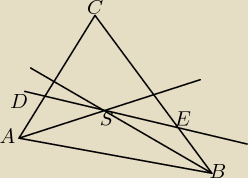
Na rysunku obok półproste AS i BS są dwusiecznymi kątów trójkąta ABC oraz DE II AB. Udowodnij
że IDEI=IADI+IBEI
15 gru 19:18
BLAZEJ_505: jak to zrobić pomoże mi ktoś
15 gru 19:54
rrr:
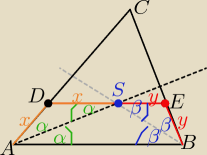
DE || AB
|∡BAS|= |∡ASD| i |∡ABS|=|∡BSE| −−− jako kąty naprzemianległe
ΔADS jest równoramienny i ΔBES też
to |DS|= x+y= |AD|+|BE|
co kończy dowód
15 gru 19:59
rrr:
oczywiście ma być: |DE|= x+y
15 gru 20:01
BLAZEJ_505: wielkie dzięki
15 gru 20:09
vfdbv: Przez punkt w w którym przecinają się dwusieczne kątów A i B trójkąta ABC prowadzimy równoległą
do boku AB. Ta równoległa przecina proste AC i BC odpowiednio w punktach M i N. Wykaż,że
|MN|=|AM|+|BN|.
26 lut 19:37
lol: lol
2 gru 12:19
lol: Nie umiem nie rozumiem a w przyszłym tygodniu test!
2 gru 12:20
niko: to jest żle
6 gru 20:09
lolololololol: lolololololololololol zle cale zadanie lololololololo
5 sty 20:59
pusia:
misia pysia elo
9 kwi 19:38
a:

25 mar 15:52
 Na rysunku obok półproste AS i BS są dwusiecznymi kątów trójkąta ABC oraz DE II AB. Udowodnij
że IDEI=IADI+IBEI
Na rysunku obok półproste AS i BS są dwusiecznymi kątów trójkąta ABC oraz DE II AB. Udowodnij
że IDEI=IADI+IBEI
 DE || AB
|∡BAS|= |∡ASD| i |∡ABS|=|∡BSE| −−− jako kąty naprzemianległe
ΔADS jest równoramienny i ΔBES też
to |DS|= x+y= |AD|+|BE|
co kończy dowód
DE || AB
|∡BAS|= |∡ASD| i |∡ABS|=|∡BSE| −−− jako kąty naprzemianległe
ΔADS jest równoramienny i ΔBES też
to |DS|= x+y= |AD|+|BE|
co kończy dowód
 misia pysia elo
misia pysia elo
