fizyka
nall:
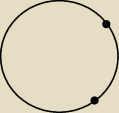
z drutu długości 1 m i oporze R1=4Ω wykonano pierścień. Jaka winna być odległość między
punktami A i B aby prąd elektryczny między nimi płynący napotykał opór R2=10Ω. Kropki to
odpowiednio punkty A i B
15 gru 19:15
Sławek:
To zadanie z tymi danymi
R1=4Ω, R2=10Ω
jest nierozwiązywalne.
15 gru 21:11
Sławek:
Masz połączenie równoległe dwóch odcinków pierścienia o oporach proporcjonalnych do długości.
r
ab + r
ba = 4Ω = R1
l
ab + l
ba = 1 m
15 gru 21:56
diss1: to zadanie ma w treści R1=100Ω
15 gru 22:58
iks:
Mamy układ równań z 2 niewiadomymi
R
1 = r
ab + r
ba
wyznaczamy np. r
ab
r
ab2 − r
abR
1 + R
1R
2 = 0
r
ab2 − 100r
ab + 1000 = 0
r
ab1 = 11,27Ω
r
ab2 = 88,73Ω
układamy proporcję dla tych dwóch rozwiązań:
stąd
pierwsze rozwiązanie
| | 11,27 | |
x1 = |
| *100 = 11,27 cm |
| | 100 | |
drugie rozwiązanie
| | 88,73 | |
x2 = |
| *100 = 88,73 cm |
| | 100 | |
16 gru 10:44
nall: dziękuję bardzo
16 gru 17:16
Tomczak: iks, skąd bierzemy ten układ równań pierwszy? Jeśli prąd płynie od A do B to te kawałki drutu
są ze sobą połączone równolegle, a R1 to chyba opór całkowity tego pierścienia, więc nie z
tego wzoru chyba trzeba to wyliczyć...
18 gru 17:47
Sławek:
Stąd: z drutu długości 1 m i oporze R1=4Ω wykonano pierścień
18 gru 19:10
Sławek:
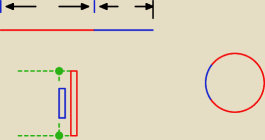
18 gru 19:19
troll : Skąd bierze się to R2?
18 gru 21:03
Sławek:
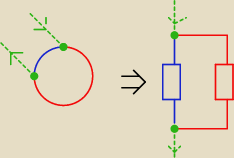
18 gru 21:19