Witam, mam uprościć wyrażenie. Nie mam koncepcj jak do tego podejść.
Grzegorz: | √a − 2√a + 1 | | 4√a + 1 | |
| : |
| + 1 |
| √a − 24√a + 1 | | 4√a − 1 | |
14 gru 23:15
rrr:
a−2√a+1= (√a−1)2 √a−24√a+1= (4√a−1)2
14 gru 23:18
ewelina: musisz pozbyć sie pierwiastków np. √a = a0,5
14 gru 23:20
rrr:
i jeszcze 4√a−1= (√a−1)(√a+1)
14 gru 23:22
Grzegorz: czyli (√a−1)2 jest równe (√a−1)(√a+1) zaś (4√a−1)2 jest równe (4√a−1)(4√a+1)
14 gru 23:24
beti: Nieee
Czy w liczniku pierwiastek jest nad całością?
14 gru 23:27
Grzegorz: tak
14 gru 23:29
rrr:
poprawiam tak ma być (4√a−1)(4√a+1)= √a−1
14 gru 23:33
beti: no to chyba to leci tak:
| √(√a−1)2 | | 4√a−1 | |
| * |
| +1= |
| (4√a−1)2 | | 4√a+1 | |
14 gru 23:33
beti: i jesli nie wiadomo, jakie jest a, to:
| | |√a−1| | | | 1+1=2, gdy a>1 | | | −1+1=0, gdy 0<a<1 | |
| |
= |
| +1= | |
| | √a−1 | | |
14 gru 23:37
rrr:
i ostatecznie
= 2
14 gru 23:38
Grzegorz: a możecie to rozpisać bo nie bardzo łapię dzięki
14 gru 23:55
rrr:
| | √a−1 | |
dla a>1 |
| +1=1+1=2 |
| | √a−1 | |
| | −(√2−1) | |
dla a∊(0,1) |
| +1= −1+1=0 |
| | √2−1 | |
15 gru 00:01
Grzegorz: Ok.ale chodzi mi o to jak doszedłeś do tego wyniku
15 gru 00:06
rrr:
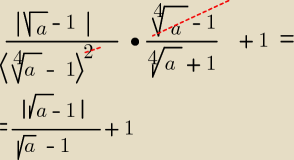
bo
(
4√a−1)*(
4√a+1)=
√a−1
15 gru 00:15
beti: Skracasz licznik drugiego ułamka z kwadratem w mianowniku drugiego ułamka. Następnie wymnażasz
oba ułamki stosując w mianowniku wzór skróconego mnożenia: (a−b)(a+b)=a2−b2 a w liczniku _
własność wartości bezwzględnej: √a2=|a|
15 gru 00:17
Grzegorz: teraz już wiem kurde zgubił mnie ten moduł.Dzięki rrr
15 gru 00:19
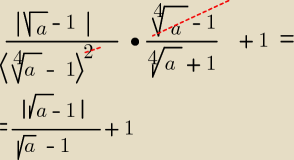 bo
(4√a−1)*(4√a+1)= √a−1
bo
(4√a−1)*(4√a+1)= √a−1