proszę o policzenie krok po kroku
natiii0900: 1. Długość każdej krawędzi ostrosłupa prawidłowego czworokątnego jest róna 6cm. Oblicz objętość
i pole powierzchni całkowitej tego ostrosłupa.
2. Oblicz pole powierzchni całkowitej i objętość stożka (z dokładnością do całości), w którym
kąt rozwarcia ma 70(stopni), a wysokość jest równa 10.
3. Do garnka o średnicy 18cm nalano wody, a następnie wrzucono brzoskwinię o średnicy 6cm. O
ile centymetrów podniósł się poziom wody w garnku ? Przyjmujemy, ze brzoskwinia jest kulą i
zanurzyła się całkowicie, oraz że z garnka nie wylała się ani kropla wody.
4. Podstawą graniastosłupa prostego jest trapez prostokątny, którego podstawy mają długość
3cm i 8cm. Krótsza przekątna graniastosłupa jest równa 12 cm i tworzy z płaszczyzną podstawy
kąt 30(stopni). Oblicz objętość tego graniastosłupa.
14 gru 16:19
dero2005:
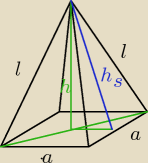
a = l = 6
I
2 = (
a2)
2 + h
s2
6
2 = 3
2 + h
s2
36 − 9 = h
s2
h
s2 = 27
h
s =
√27 = 3
√3
h
2 = h
s2 − (
a2)
2
h
2 = (3
√3)
2 − 3
2
h
2 = 27 − 9 = 18
h =
√18 = 3
√2
P
b = 2*a*h
s = 2*6*3
√3 = 36
√3
P
p = a
2 = 6
2 = 36
P
c = P
b + P
p = 36(1+
√3) cm
2
V =
13P
p*h =
13*36*3
√2 = 36
√2 cm
3
14 gru 17:05
dero2005:
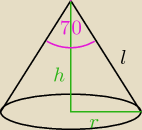
h = 10
r = h* 0,7002 = 10*0,7002 = 7
z pitagorasa
l
2 = h
2 + r
2 = 10
2 + 7
2 = 100 + 49 = 149
l =
√149
P
c = πr(r+l) = π*7(7+
√149) = 49π + 7π
√149 = 422,37 = 422 [j
2]
V =
13πr
2*h =
13π*7
2*10 = 512,86 = 513 [j
3]
14 gru 18:32
dero2005:
Objętość brzoskwini
r = 3 cm → pormień brzoskwini
| | 4 | | 4 | |
Vk = |
| πr3 = |
| π33 = 36π
|
| | 3 | | 3 | |
| | Vk | | 36π | | 4 | |
h = |
| = |
| = |
| cm podniósł się pozim wody w garnku,
|
| | πR2 | | π*92 | | 9 | |
gdzie R = 9, promień garnka
14 gru 19:02
dero2005:
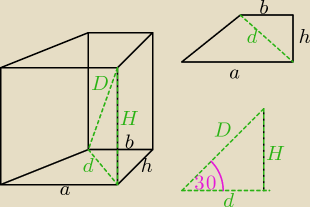
a = 8 cm
b = 3 cm
D = 12 cm
liczymy przekątną podstawy d
| | √3 | | √3 | |
d = D* |
| = 12 |
| = 6√3 cm
|
| | 2 | | 2 | |
liczymy wysokość podstawy h z pitagorasa
h =
√d2 − b2 =
√(6√3)2 − 32 =
√108 − 9 =
√99 = 3
√11 cm
liczymy pole podstawy
| | a+b | | 8+3 | | 33 | |
Pp = |
| *h = |
| *3√11 = |
| √11 cm2
|
| | 2 | | 2 | | 2 | |
liczymy wysokość graniastosłupa H z pitagorasa
H =
√D − d2 =
√122 − (6√3)2 =
√144 − 108 =
√36 = 6 cm
liczymy objętość
| | 33 | |
V = Pp*H = |
| √11*6 = 99√11 cm3
|
| | 2 | |
14 gru 19:35