rozwiąż nierówność
Edzio: Rozwiąż nierówność:
f(1/x)≤f(x)
13 gru 21:28
Edzio: Proste równanie, nikt nie wie

13 gru 22:43
Święty: Jak proste to czemu nie zrobisz?
13 gru 22:45
krystek: ?
13 gru 22:45
ZKS:
To jest cała treść zadania?
13 gru 22:48
Edzio: Ups, faktycznie jeszcze coś było na początku: O funkcji f: R →R wiadomo że jest rosnąca.
Próbowałem rozwiązać, ale wychodzi mi x ∊(−∞;0)∪<1;∞), a ma wyjść x ∊<−1;0)∪<1;∞)
13 gru 23:20
aa: napisz tu swoje "próby"
13 gru 23:26
Edzio: Nie jestem właściwie pewien czy w taki sposób powinno się to zadanie rozwiązywać, ale
wcześniejsze 2 przykłady wyszły mi dobrze.
1/x≤x
1≤x2
1−x2≤0
(1−x)(1+x)≤0
i stąd wyszło x ∊(−∞;−1)∪<1;∞)
13 gru 23:36
ZKS:
A skąd wiesz że x jest dodatni że sobie tak mnożysz przez niego?
13 gru 23:40
Edzio: Nie wiem, więc jak inaczej to rozwiązać

13 gru 23:42
ZKS:
Przenieś x na lewą stronę doprowadź do wspólnego mianownika i przemnóż obustronnie przez
kwadrat mianownika.
13 gru 23:44
aa: D: x≠0 D=R/{0}
(1−x
2)x≤0
(1−x)(1+x)x≤0
i ustalenie przedziałów pamiętając o dziedzinie
13 gru 23:46
Edzio: Wyszło x(1−x)(1+x)≤0, czyli miejsca zerowe {0,1,−1} i D=R\{0}, tylko że dalej nie wiem co z
tym zrobić
13 gru 23:52
ZKS:
Nigdy nie rozwiązywałeś nierówności wielomianowej?
13 gru 23:53
aa:
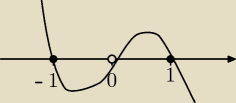
x∊<−1, 0)v<1, +
∞)
14 gru 00:01
Edzio: Zapomniałem sobie że coś takiego w ogóle istnieje(mam teraz powtórkę przed maturą), dzięki za
przypomnienie, już wiem jak rozwiązać

14 gru 00:02
ZKS:
To ciężko będzie z maturą jak tak.

14 gru 00:05


 x∊<−1, 0)v<1, +∞)
x∊<−1, 0)v<1, +∞)

