romb
Monia: w rombie ABCD bok AB ma dł 13, a przekątna AC ma dł 24. Oblicz cosinus kąta BD
13 gru 19:50
Monia: pomocy...proste zadanie ale nie moge wpasc na pomysl
13 gru 19:56
beti: jakiego kąta?
13 gru 20:04
Monia: kąta DAB
13 gru 20:05
Monia: pomyliłam sie...mozesz pomoc? bo nie mam pomyslu
13 gru 20:05
beti: z tw. cosinusów:
242=132+132−2*13*13*cosα
13 gru 20:10
Monia: a cos bez twierdzenia cosinusow? nie mialam jeszcze tego
13 gru 20:11
Monia: a po za tym wynik tutaj z tego twierdzenia jest zły..
13 gru 20:15
Monia: na pewno jest tu ktos madry kto wie jak to zrobic..
13 gru 20:17
Monia:
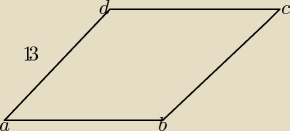
13 gru 20:19
beti: nie jest zły, tylko kąt DAB jest rozwarty. Znasz wzory redukcyjne? bo nimi trzeba teraz
wyznaczyć miarę kąta. Inna metoda też tak wychodzi
13 gru 20:23
Monia: | | 119 | |
w odp w podreczniku mam ze cos DAB= |
| |
| | 169 | |
13 gru 20:24
Monia: jak rozwarty... chyba ostry?
13 gru 20:24
beti: O sorry... przyjęłam, że 24 to przekątna DB
13 gru 20:31
beti: No tak. Najpierw oblicz druga przekątną z tw. Pitagorasa (|BD|=10), a potem już tw. cosinusów:
102=132+132−2*13*13*cosα. Teraz wyjdzie.
13 gru 20:35
beti: | | α | | α | |
Inna metoda, to oblicz sin |
| i cos |
| i wykorzystaj wzór:
|
| | 2 | | 2 | |
| | α | | α | |
cosα=cos2 |
| − sin2 |
| . |
| | 2 | | 2 | |
13 gru 20:38
mm:
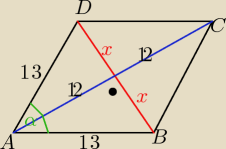
x
2=13
2−12
2 ⇒x=5 |BD|=10
z tw. cosinusów
| | 132+132−102 | |
cosα= |
| =.... to już dokończysz? |
| | 2*13*13 | |
13 gru 20:40